Considere dois reatores de reservatório sob agitação em série com reciclo mostrado abaixo:
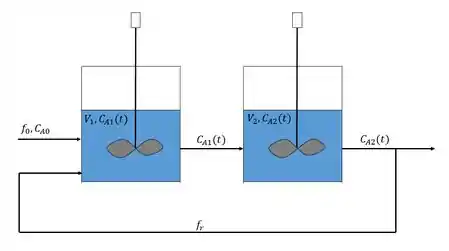
Você pode supor o seguinte:
- Cada reator está perfeitamente misturado e a temperatura é constante.
- Os volumes, e , são constantes e tabém as densidades das misturas que estão reagindo.
- O fluxo de entrada, , e o fluxo de reciclo, , são constantes.
- A reação química é basicamente de primeira ordem, e a taxa de ração é dada por .
- Os reatores estão inicialmente em estado estacionário com uma concentração de entrada .
- O retardo de transporte entre os reatores é desprezível.
Determine o modelo matemático para a concentração de no primeiro e no segundo reator.
Passo 1
Vamo fazer o balanço molar para o componente no primeiro reator:
O componente é um reagente do processo, logo ele é consumido e a expressão do balanço fica:
Vamos escrever termo a termo:
A corrente de saída é a soma das duas correntes de tanque que entram no primeiro reator, isso porque os volumes dos reatores são constantes.
Juntando tudo:
Passo 2
O balanço para o segundo reator:
Fazendo termo a termo:
Juntando tudo: