A seguite reação elementar irreversível ocorre no reator elementar mostrado abaixo:
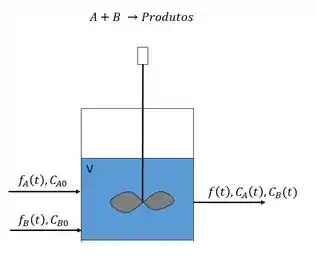
A velocidade de consumo do regemnte é dada por:
O conteúdo do reator está perfeitamente misturadao e a temperatura, o volume e a densiadade da mistura reagida podem ser consideradas constantes.
Suponha que as concentrações de entrada, , são constantes. Obtenha o modelo matemático para essas concentrações em função dos fluxos de entrada.
Passo 1
Dessa vez, em vez de fazer o balanço de massa, vamos fazer o balanço molar para o componente (que dá no mesmo no fim das contas)
O componente é um reagente do processo, logo ele é consumido e a expressão do balanço fica:
Vamos escrever cada parcela do balanço separadamente:
Juntando tudo:
Passo 2
Como o volume do tanque é constante, o que entra é igual ao que sai, sendo assim:
Subtitindo na expressão:
Passo 3
A gente já tá quase lá. O problema é que encontramos o EDO não linear, isso acontece porque existem termo com produtos de funções que dependem do tempo, e por isso precisamos linearizá-las.
A linearização ficará assim:
Os termos com barra representam o valor daquela variável em .
Caso você não se lembre como fazer a linearização, dá uma revisada nesse assunto porque é bem importante.
Substituindo na EDO:
Passo 4
Agora, ficamos com uma EDO não-homogênea por causa das constantes solta. Precisamos inserir então as variáveis desvio. A nossa EDO tá assim:
Vamos reescrever essa EDO com todas as variáveis com o valor inicial:
Definindo as variáveis desvio e fazendo a primeira menos a segunda, teremos:
Rearranjando:
Para o componente , a resolução é de forma análoga: