A seguite reação elementar irreversível ocorre em um reator CSTR mostrado abaixo:
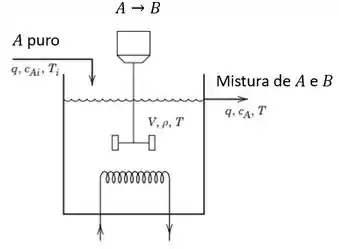
A velocidade de consumo do regente é dada por:
O conteúdo do reator está perfeitamente misturadao e a temperatura, o volume e a densiadade da mistura reagida podem ser consideradas constantes. A vazão de entrada, , também é constante.
Encontre a função de transferência . Onde e são as variáveis desvio de e .
Passo 1
Começando pelo balanço material para o componente :
O componente é um reagente do processo, logo ele é consumido e nada é gerado, a expressão do balanço fica:
Vamos escrever cada parcela do balanço separadamente:
Como o tanque está bem misturado, a concentração da saída é igual à do próprio tanque, e como volume é constante, a vazão de entrada é igual à de saída:
A taxa dado é em base volumétrica, logo, precisamos multiplica-la pelo volume do tanque:
Juntando tudo:
Passo 2
O nosso modelo matemático já está pronto, entretanto, o exercício pede a função de transferência o que significa que precisamos trabalhar um pouquinho mais em cima da nossa EDO.
Reorganizando a EDO:
Devemos então aplicar a transformada de Laplace na expressão, mas antes, devemos sempre alicar as variáveis desvio na EDO.
Vamos reescrever toda a equação com suas funções de tempo no estado estacionário () e vamos representar isso com uma barra sobre a variável:
Fazendo :
Definindo as variáveis desvio e substituindo em , teremos:
Nesse caso a nossa EDO não mudou muito, porque se trata de uma EDO homogênea. Entretanto, mesmo quando estamos trabalhando com EDO’s Homogêneas, é bom aplicar as variáveis desvio.
Passo 3
Agora que já aplicamos as variáveis desvio, já podemos usar transformada de Laplace na nossa EDO:
Transformadas de Laplace é um tópico muito importante e para achar fuções de transferência ele é primordial. Caso você não se lembre como alicar essa operação, seria uma boa ideia dar uma revisada nesse conteúdo.
Prosseguindo: vamos colocar em evidência:
Por fim, a função de transferência