Dois tanques são conectados conforme ilustrado na figura abaixo:
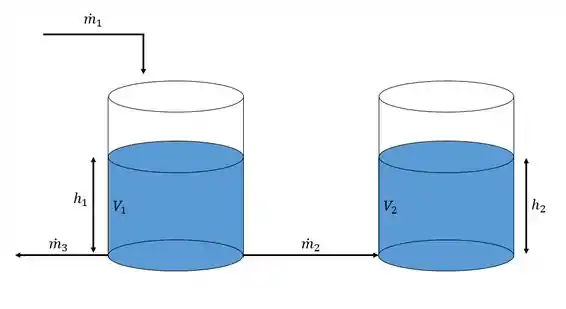
Desenvolva o modelo matemático para esse sistema de maneira a encontrar a variação do nível dos tanques e .
Passo 1
Vamos começar pelo primeiro tanque. O primeiro passo é sempre começar pelo balanço de massa:
Podemos desconsiderar os dois últimos termos porque não tem reação no tanque e portanto, nada é gerado nem consumido.
O termo de acúmulo a gente sempre representa como a derivada, a corrente entra no tanque e as correntes e saem do tanque:
Substituindo tudo no balanço:
Entretanto o exercício pede que a gente encontre a expressão de variação de , e não de . Sendo assim, precisamos fazer algumas substituições. Sabendo que:
E
Logo:
Substituindo na EDO:
Considerando a área e a densidade constante, teremos:
Passo 2
Vamos fazer o mesmo para o segundo tanque agora.
O segundo tanque também não tem nenhum consumo nem geração, mas também não tem nenhuma corrente entrando, sendo assim:
Como a única corrente que entra no segundo tanque é a corrente , o balanço ficará assim:
Agora vamos fazer o mesmo procedimento que fizemos para o primeiro tanque para encontrar a expressão de :
Portanto:
Considerando e constantes, teremos: