Considere um tanque com fluxo de reciclo (recirculação)mostrado na figura abaixo. Objetiva-se estudar a dinâmica do nível , de acordo com o fluxo de entrada, , e a abertura das válvulas, . Considere densidade, , a área do tanque, , e a vazão de saída, , como constantes. Obtenha o modelo matemático do processo.
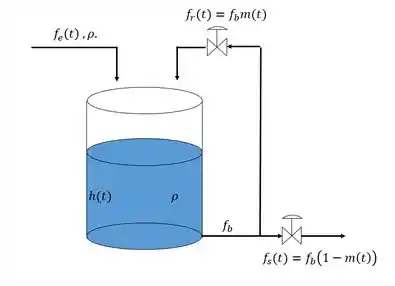
Passo 1
Vamos começar fazendo o balanço de massa para esse tanque então:
Não existe reação no processo, portanto os termos de reação e consumo serão nulos.
Passo 2
Vamos colocar tudo em termos de volume:
Substituindo tudo
Podmeos então cancelar em toda a equação.
Precisamos da expressão para a altura do nível no tanque, então:
Passo 3
Tamo quase lá, mas o exercício também pede para que a gente relacione o nível do fluido no tanque com a abertura da válvula, . Como:
Passo 4
Repare que caímos numa EDO não-homogênea, isso é, ela apresenta uma constante, . Quando acontece isso, precisamos aplicar variáveis desvio.
Atualmente, nossa EDO é a seguinte:
Vamos reescrever essa EDO colocando todas as variáveis com seus valores no estado inicial:
Como é uma constante, seu valor não se altera. Agora, nós subtraímos a segunda expressão da primeira:
Vamos definir as nossas variáveis desvio:
Substituindo na EDO:
Conseguimos então transformar uma EDO não-homogênea em uma EDO homogênea.