Encontre a função de transferência
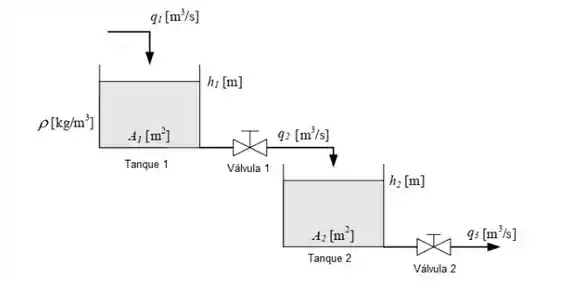
Sabe-se que:
Considere constante.
Passo 1
Vamos começar pelo primeiro tanque. O primeiro passo é sempre começar pelo balanço de massa:
Podemos desconsiderar os dois últimos termos porque não tem reação no tanque e portanto, nada é gerado nem consumido.
O termo de acúmulo a gente sempre representa como a derivada, a corrente entra no tanque e as correntes e saem do tanque:
Substituindo tudo no balanço:
Mas:
E:
Substituindo no balanço, e simplificando :
Passo 2
Vamos reorganizar a equação e passar tudo que tem para o lado esquerdo:
Antes de aplicarmos a transformada de Laplace devemos fazer a inserção das variáveis desvio.
Reescrevendo a equação acima no estado estacionário ()
Fazendo a de cima menos a de baixo:
Definindo as variáveis desvio e substituinto na EDO:
Passo 3
Aplicando Laplace:
Isolando :
Por fim:
Passo 4
Agora devemos fazer o mesmo para o segundo tanque. O desenvolvimento é praticamente igual, sendo assim, vamos pular algumas etapas.
Do balanço de massa:
Substituindo e simplificando :
Rearranjando a equação:
Aplicando variáveis desvio:
Aplicando Laplace:
Passo 5
O exercício pede a função de transferência , entretanto, temos:
Ou seja, se multiplicarmos as duas funções de transferências, conseguiremos a resposta que desejamos:
Logo: