Água quente a uma vazão de (constante) e temperatura é misturada com água fria a uma vazão constante de e uma temperatira constante de . Ambos os fluxos fluem para uma banheira, mas por motivo de descuido a água está transbordando e mantendo a banheira cheia de água . O volume da banheira é de . Supondo que a água na banheira está perfeitamente misturada, deduza a equação diferencial que relaciona a temperatura da banheira à temperatura da água quente, Obtenha a fução de transferência .
Passo 1
Começando pelo clássico balanço de energia.
Para esse caso, não temos nenhuma fonte de geração ou consumo de energia. Sendo assim, o balanço de enregia pode ser reduzido a:
Na nossa banheira, vamos considerar separadamente duas correntes entrando e uma corrente saindo.
Para a entrada, teremos a corrente quente a corrente fria. Sendo assim:
Como:
Para a saída, iremos considerar uma corrente que é a soma das duas correntes de entrada.
Para esse problema, estamos considerando parâmetros concentrados, o que quer dizer que a temperatura na banheira é igual em todos os pontos e igual à temperatura de saída. Além disso consideraramos densidade e capacidade calorífica constantes e que não exitem perdas no sistema.
Por enquanto, estamos assim:
Ou:
O acúmulo de energia no sistema é dado por:
Juntando tudo:
Passo 2
Antes da gente continuar, precisamos dar uma ajeitada na casa.
Primeiramente vamos organizar a EDO passando tudo que tem para a esquerda da equação.
Também precisamos passar nossa EDO para variáveis desvio. Vamos, então, reescrever a equação com todas as variáveis no valor inicial (e vamos representar isso com uma barra).
Fazendo (, teremos:
Repare que como a temperatura e a vazão da corrente fria são constantes, os termos referentes à essa corrente se anulam.
Definindo as variáveis desvio:
Substituindo em :
Passo 3
Casa arrumada, podemos prosseguir. O próximo passo é a transformada de Laplace.
Aplicando Laplace em teremos:
A transformada de Laplace é uma parte muito importante da resolução desse exercício. Se você não tá com esse assunto afiado, seria bacana dar uma revisada nesse tópico!
Rearranjando:
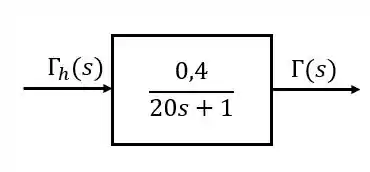
Portanto, a função de transferência será:
Ou:
Substituindo os valores:
E o diagrama de blocos:
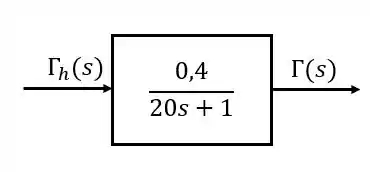
Resposta