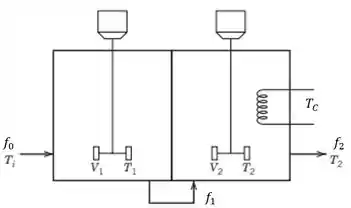
Um reator agitado completamente isolado com dois compartimentos é mostrado na figura abaixo. A ideia básica é alimentar os reagente continuamente no primeiro compartimento, onde eles serão preaquecidos pela energia liberada na reação exotérmica, que é esperado que se ocorra principalmente no segundo compartimento. A parede entre os dois compartimentos é consideravelmente fina, permitindo a troca térmica; o reator pode ser considerado perfeitamente isolado; e existe uma serpentina de resfriamento no segundo compartimento para remover o excesso de energia liberada na reação. Ambos os tanques estão completamente cheios o tempo todo.
Inicialmente serão realizados alguns testes com alimentação de um único componente (sem reação) para avaliar as características térmicas do reator.
Desenvolva o modelo matemático para esse processo sob as condições de nenhuma reação. Assuma que , e podem variar.
Passo 1
O exercício pede o modelo matemático que descreve o processo, isso quer dizer que ele quer as EDO’s que mostram como a temperatura varia no tanque. Como temos dois compartimentos precisaremos de duas EDO’s.
Começando pelo começo. Balanço de energia para o primeiro compartimento:
O enunciado pediu para considerarmos que não existe nenhuma reação, logo, o balanço de massa para o primeiro compartimento fica:
Nós temos uma corrente entrando e uma corrente saindo do primeiro compartimento e além disso ainda temos troca térmica por convencção com o segundo compartimento.
A quantidade de calor trocada por convecção será:
Onde é a área da parede que divide os dois compartimentos e é o coeficiente de troca térmica global por convecção do material da parede.
O nosso balanço tá assim por enquanto:
Porém, o enunciado diz que ambos os compartimentos estão sempre cheio, isso quer dizer que as vazões são sempre iguais. Portanto:
Mas como:
Juntando tudo:
Ou:
Passo 2
Agora podemos partir para o segundo compartimento.
O segundo compartimento, assim como o primeiro, também não possui reação química. Portanto:
No segundo compartimento além as entrada e saída de energia através das correntes, e da troca térmica por convecção pela parede com o primeiro compartimento, também teremos troca térmica por convecção com a serpentina.
O calor trocado com a serpentina será:
Onde é a área de troca térmica da serpentina e é o coeficiente de troca térmica global por convecção do material da serpentina.
Portanto, nosso balanço ficará:
Mas assim como no primeiro compartimento, o segundo compartimento permanece cehio o tempo todo, o que indica que a vazão de entra é igual a vazão de saída.
Sendo assim:
Por fim:
Juntando tudo:
Ou: