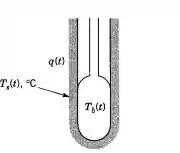
Considere o sensor de temperatura esboçado na figura abaixo. O bulbo e sua fonte térmica vizinha estão em uma temperatura uniforme , e a vizinha está em uma temperatura uniforme . A troca de calor entre a vizinhança e o bulbo é dada por:
Onde:
proporção de transferência de calor,
coeficiente de calor de convecção do filme,
área entre o bulbo e sua vizinhança
Considere , a massa do bulbo e da fonte térmica, e , sua capacidade calorífica. Obtenha a função de trsnferência que descreve a a resposta de temperatura do bulbo quando a temperatura da vizinhança varia. Liste todas as suposições e desenhe o diagrama de blocos para o bulbo.
Passo 1
Antes de começar, devemos fazer nossas suposições.
Para fazer a modelagem desse bulbo, existem duas coisas que devemos considerar principalmente. Primeiro que o o bulbo se encontra a parâmetros concentrados, ou seja, a temperatura em qualquer parte do bulbo é a mesma.
Segundo, devemos considerar que não existem perdas. Toda e qualquer troca de energia acontece exclusivamente do bulbo para a vizinhança ou da vizinhança para o bulbo.
Passo 2
Vamos começar fazendo o balanço de energia para a temperatura no bulbo:
Para esse caso, não temos nenhuma fonte de geração ou consumo de energia. Sendo assim, o balanço de enregia pode ser reduzido a:
A relação entre a quantidade de energia que entra e sai do nosso sistema (bulbo) já foi dada do enunciado:
Logo:
E o Acúmulo de enercia:
Por fim:
Passo 3
Antes de prosseguir, vamos rearranjar a EDO para conseguir trabalhar mais facilmente com ela. Sendo assim, vamos colocar todos os termos com do lado esquerdo da equação.
Além disso, precisamos ainda passar as nossas variáveis para variáveis desvio. Para isso, vamos reescrever a equação com todos as variáveis no estado inicial (vamos representar com uma barra):
Fazendo :
Agora, vamos definir nossas variáveis desvio:
Fazendo as substituições:
Passo 4
Agora já está tudo pronto para podermos prosseguir para o próximo passo que é a aplicação da transformada de Laplace.
Aplicando Laplace em teremos:
A transformada de Laplace é uma parte muito importante da resolução desse exercício. Se você não tá com esse assunto afiado, seria bacana dar uma revisada nesse tópico!
Rearranjando:
Portanto, a função de transferência será:
Ou:
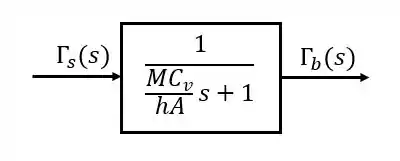
E o diagrama de blocos:
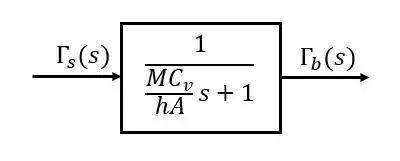
Resposta