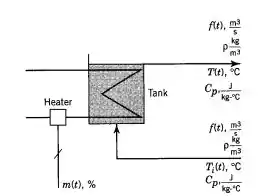
Considere o reservatório aquecido mostrado na figura abaixo. Um fluxo de processo está sendo aquecido no reservatório por um aquecedor elétrico. A proporção da transferência calorífica, para o fluido de processo está relacionado ao sinal, , por:
Você pode supor que o reservatório de aquecimento está bem isolado, que o fluido está bem misturado no reservatório e que a capacidade calorífica e a densidade do fluido são constantes. Desenvolva o modelo matemático que descreva como a temperatura de entrada, , o fluxo do processo, , e o sinal, , afetam a temperatura de saída . Depois determine as funções de transferência e esboce o diagrma de blocos.
Passo 1
Nesse exercício o enunciado foi bonzinho e já fez todas as considerações necessárias. Então vamos direto pro balanço de energia porque a gente tá sem tempo, irmão.
Aqui, além das correntes de entrada e saída do reservatório, também teremos uma taxa de geração de energia promovido pelo aquecedor elétrico.
Vamos escrever as expressões para cada um dos termos acima:
E o enunciado nos deu a expressã da energia do gerador elétrico:
Juntando tudo:
Passo 2
E olha só. De novo caímos em uma EDO não linear. Isso acontece porque temos dois termos onde temos duas funções de tempo se multiplicando. Precisamos resolver isso.
Para fazer essa linearização, usaremos a linearização de Taylor. Quando temos um caso como esse de produto de funções, a linearização é feita da seguinte forma:
Primeiro a gente escreve a função em torno do ponto onde estamos linearizando, depois nós vamos derivar a função duas vezes, uma vez em relação a cada função que compõe a função principal.
Sendo assim:
E analogamente:
Substituindo no balanço
Passo 3
O próximo passo é colocar a nossa expressão em variáveis desvio. Para isso, vamos escrever a expressão com todos os termos em seus estados iniciais.
Olha só, a maioria dos termos se anulou porque as diferenças ficaram igual a . Fazendo :
Quando fazemos os termos que são puramente constantes se anulam e sobram apenas os que são função do tempo.
Vamos definir nossas variáveis desvio:
Substituindo em :
Rearranjando:
Passo 4
Agora, vamos passar tudo que depende de para a esquerda:
Show! Agora já podemos aplicar Laplace:
Colocando em evidência:
Por fim:
Passo 5
Agora só nos resta esboçar o diagrama de blocos.
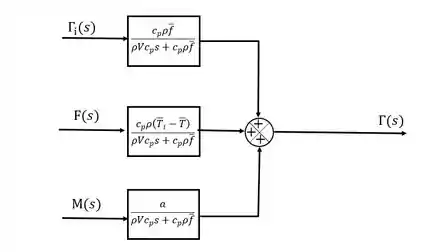
Como a saída depende de três entradas que estão se somando:
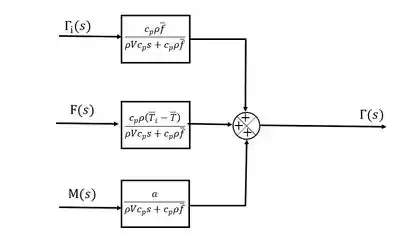
Resposta