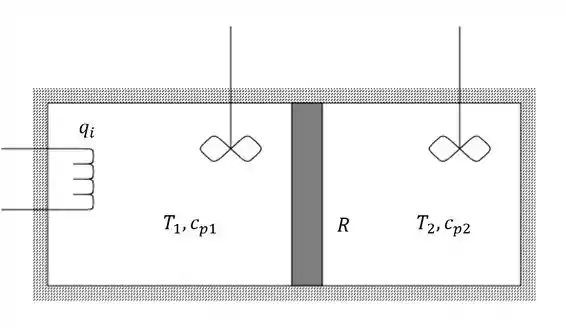
Considere um sistema fechado composto por duas câmaras separadas por uma parede de resitência térmica . A câmara da direira tem temperatura e capacidade calorífica , e a câmara da esquerda tem temperatura e capacidade calorífica . A câmara da direita é aquecida por uma serpentina que fornece calor a uma taxa . Encontre o modelo matemático que rege o sistema. Considere que os dois compartimentos estão bem misturados.
Passo 1
Para encontrar o modelo mademático que descreve o sistema, devemos encontrar o conjunto de EDO’s que governam a temperatura em cada um dos compartimentos.
Começaremos então pelo primeiro compartimento. Vamos fazer isso analisando o balanço de energia para ele:
Os termos de geração e consumo servem para representar as taxas de calor quando temos reações químicas no sistema. Não é o caso aqui.
Na primeira câmara nós temos enegia entrando no sistema através da serpentina. O enunciado diz que essa energia é passada para o fluido a uma taxa , sendo asism:
O primeiro compartimento também troca energia com o segundo compartimento. Pela Lei de Fourier essa troca de energia acontece da seguinte maneira:
Onde é a resistência proporcionada pela parede. Sendo assim a energia que sai da primeira câmara é:
A variação de energia no primeiro compartimento também pode ser descrita como:
Juntando tudo:
Passo 2
Para o segundo compartimento, a única troca de energia que existe é com o primeiro compartimento, então: