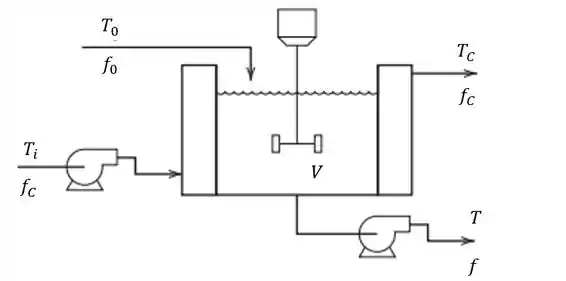
Um tanque encamisado mostrado abaixo é usado para esfriar uma corrente de processo. As seguintes informações são sabidas:
- O volume de líquido no tanque, , e o volume de fluido refrigerante na camisa, , permanencem constantes. A vazão volumétrica permanece constante mas varia com o tempo.
- As perdas de energia da camisa são desprezíveis.
- Os conteúdos do tanque e da camisa podem ser considerados bem misturados e têm capacitância térmica considerável.
- As capacitâncias térmicas da parede do tanque e da camisa são desprezíveis.
- O Coeficiente global de troca térmica por convecção entre o líquido do tanque e o fluido refrigerante varia com a vazão na camisa:
Desenvolva o modelo matemático para o sistema.
Passo 1
O exercício pede o modelo matemático que descreve o sistema, ou seja, precisamos encontrar expressões matemáticas que ilustrem o comportamento da temperatura tanto no tanque quanto na camisa.
Para fazer isso, além de todas considerações já expostas no enunciado, vamso ainda considerar que a densidade e o calor específico de ambos os fluido podem ser considerados constantes.
Vamos começar fazendo o balanço para o líquido do tanque.
Nesse process não existe nenhuma reação que gera ou consome energia, logo o balanço de energia pode ser reduzido:
Além das correntes de entrada e saída, o líquido do tanque troca energia por convecção com o líquido da camisa. A quantidade de calor trocada por convecção será:
Onde é a área de troca térmica entre os dois compartimentos e é o coeficiente de troca térmica global por convecção.
Entretanto, o enunciado diz que o valor de varia de acordo com a quantidade de fluido na camisa da seguinte forma:
Logo:
Colocando tudo no balanço
Temos um termo referente à corrente de entrada, outro referente à corrente de saída e um terceiro referete à troca térmica proporcionada pela camisa.
Porém, como o volume do tanque é constante, podemos assumir que:
Sendo assim:
O termo de acúmulo de energia pode ser escrito como:
Logo
Passo 2
Agora precisamos fazer o mesmo procedimento para a camisa:
O fluido da camisa também não faz nenhuma reação, portanto:
Para a camisa, a montagem do balanço vai ser análoga à do tanque, uma vez que ela também apresenta uma corrente de entrada, uma corrente de saída e troca térmica por convecção com o fluido que está dentro do tanque. Sendo assim:
A única diferença é que o sinal da expressão referente à troca térmica por convecção é trocado, uma vez que um fluido recebe energia e o outro fornece.
Obs: repare que a resposta encontrada foi uma EDO não linear, já que temos uma função de tempo () elevada a . Caso fosse necessário aplicar transformada de Laplace para encontrar a função de transferência do processo, precisaríamos linearizar esse termo, porém, como o exercício pede apenas o modelo matemático do sistema, as EDO’s encontrada são a resposta do exercício.