Um tanque completamente fechado e cheio de um fluido com capacidade calorífica , densidade e volume é aquecido por uma serpentina. Um fluido que passa pela serpentina tem temperatura e vazão . Considere que a área da serpentina é igual a e que o coefiente global de troca térmica por convecação é proporcional à vazão do fluido da serpentina. O tanque pode ser considerado bem agitado e está completamente isolado, a densidade, volume e capacidade calorífica são constantes. Encontre a função de transferência .
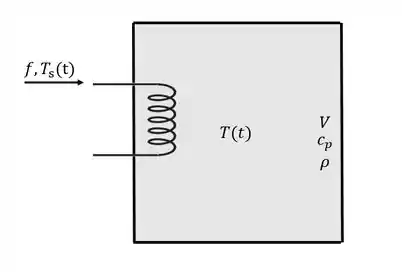
Passo 1
Seguinte, vamos começar com o clássico balanço de energia:
Nesse caso, a única fonte de energia que a gente tem é a energia proveniente da serpentina. Não temos nenhuma corrente de entrada nem de saída, nenhuma perda pro ambiente já que o tanque está bem agitado e também não temos nenhuma outra fonte de energia. Então, nosso balanço pode ser reduzido a:
Onde a energia que entra é a da serpentina. O tanque troca energia com a serpentina através da convecção entre o fluido do tanque e o fluido da serpentina segundo a seguinte fórmula:
Onde é a área da serpentina e o coeficiente global de troca térmica por convecção.
O enunciado diz que é proporcional à vazão do fluido da serpentina, logo:
Onde é a razão de proporcionalidade.
Logo a energia que “entra” no sistema é:
O acúmulo de energia no sistema pode ser escrito como:
Logo, o balanço de energia será:
Rearranjando:
Passo 2
O próximo passo agora é aplicar a transformada de Laplace na nossa EDO:
Colocando em evidência:
Logo, a função de trasnfência será:
Ou: