Deseja-se bombear água a de um poço aberto, com profundidade de , à vazão de , através de um tubo de aço comercial de de diâmetro (schedule 40). Utiliza-se uma bomba que tem um NPSHR de a esta vazão. Qual é a altura máxima em relação à superfície do líquido no reservatório em que a bomba pode ser posicionada, tal que não haja cavitação?
DADOS:
- escoamento permanente, incompressível, turbulento (no duto)
Passo 1
Temos uma tubulação em que a água entra nela abaixo da superfície do líquido, que está aberta pra atmosfera. Queremos saber qual a máxima altura que a bomba pode estar da superfície do líquido para não ter cavitação.
Para não haver cavitação:
Como ele pede “a máxima altura”, vamos trabalhar no limite:
E os NPSH surgem de balanço de energia, então vamos ter que fazê-lo, certo? A questão é quais pontos escolher para o balanço, onde estarão 1 e 2.
Um dos pontos no balanço vai ter que ser o bocal de sucção, pois é nele que você estabelece ter uma determinada carga mínima pra não cavitar, que é a medida do NPSHR. E o outro ponto, nesse problema, é conveniente ser a superfície do líquido, porque você sabe que a pressão é a atmosférica e que, como é a superfície de um RESERVATÓRIO, a velocidade ali é aproximadamente zero. Daí:
Passo 2
Escrevendo o balanço de energia entre os pontos 1 e 2:
E, fazendo as simplificações:
- Estamos analisando de 1 até a entrada da bomba, então o líquido ainda não recebeu o trabalho da bomba daí:
- O ponto 1 está exposto à atmosfera daí:
- Como 1 é um ponto na superfície de um RESERVATÓRIO:
- Como o regime de escoamento é dado turbulento na tubulação:
- Lembrando que a perda de carga total é o somatório da perda de carga na tubulação reta com a perda de carga em acidentes e, como não temos informação sobre acidentes, se resume a:
Lá na teoria vimos que:
![]()
Para fazer esse termo aparecer, temos que dividir todos os termos da equação aí de cima por e subtrair dos dois lados. Fazendo isso e rearranjando:
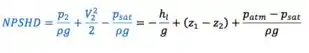
Quanto ao termo :
Sendo a velocidade dentro da tubulação; como o ponto 2 também é dentro da tubulação, . Tendo a vazão e a área transversal do tubo, achamos :
Em que é o diâmetro INTERNO do tubo.
Passo 3
Mas ainda não temos ; nos foi informado apenas “tubo de aço comercial de de diâmetro (schedule 40)”. Esse é o diâmetro nominal; precisamos consultar uma tabelinha:
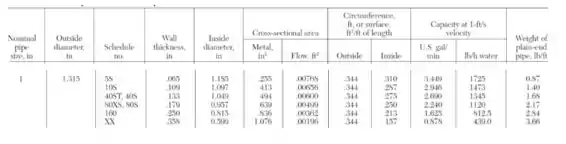
Repara que para o diâmetro nominal (nominal pipe size) de e , o diâmetro interno (inside diameter) é . Daí, trabalhando no SI:
E, com essa velocidade dentro do tubo, podemos calcular, logo, o número de Reynolds, que vai ser necessário para calcular o fator de atrito de Darcy, :
Também vamos precisar da rugosidade pra calcular o . Indo atrás dessa informação, que é tabelada, para o aço comercial:
Daí:
Com e , podemos ir no diagrama de Moody e achar o fator de atrito de Darcy, :
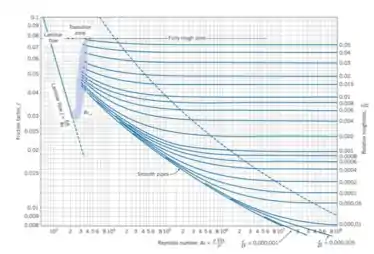
Passo 4
Voltando pra expressão do NPSHD que achamos:
Substituindo a expressão pra e chamando
Sendo que , porque é o comprimento total da tubulação.
Impondo a condição de iminência de cavitação:
Daí, substituindo todos os valores, em unidades do SI:
A única coisa que não sabemos nessa expressão é . Isolando-o e calculando-o:
Mas chamamos
E é o ponto abaixo da superfície da água, daí . Portanto:
Ou seja, a bomba tem que ficar debaixo da superfície da água para não cavitar.