Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de NPSH e Cavitação

Ver Teoria
Exercício 12345

Enunciado

Usa-se uma bomba centrífuga para transferir um solvente volátil de um tanque para outro. O solvente é um fluido newtoniano e incompressível e escoa na tubulação em regime plenamente turbulento. O relatório técnico das últimas 24 horas mostra que, às 10 horas, a referida bomba operava com carga positiva de sucção (CPS) disponível igual à requerida, e que, no referido período, a temperatura ambiente variou, conforme mostra a tabela abaixo.

Sabendo-se que os tanques, a tubulação e a bomba estão permanentemente expostos ao meio ambiente, e que as demais variáveis envolvidas permaneceram inalteradas no referido período, a bomba:

Dado: A carga positiva de sucção (CPS) corresponde ao termo da língua inglesa Net Positive Suction Head (NPSH).

  1. pode ter operado sob cavitação entre 10 h e 16 h.
  2. operou as 24 horas sob cavitação.
  3. operou as 24 horas sem cavitação.
  4. operou sob cavitação entre 0 h e 10 h e entre 16 h e 24 h.
  5. operou sob cavitação entre 2 h e 4 h.

Passo 1

Temos que fazer análise de cavitação em um fluido escoando e sabemos que tudo é constante, com exceção da temperatura ambiente. O enunciado diz também que a tubulação e a bomba estão permanentemente expostas à temperatura ambiente, então podemos dizer que quanto maior a temperatura ambiente, maior a temperatura do fluido escoando.

Apesar de não termos informações quantitativas pra fazer contas, temos uma informação qualitativa importante para 10   h :

N P S H D = N P S H R

E sabemos que essa é a condição limite de cavitação. Vamos ter que analisar se no decorrer do dia essa relação se mantém ou se um termo fica maior do que o outro. Lembrando que, para não cavitar:

N P S H D > N P S H R

Passo 2

Sabemos que às 10   h :

N P S H D = N P S H R

Escrevendo isso em termos dos parâmetros físicos:

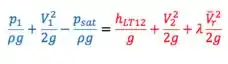
Em que:

“Mas a temperatura não aparece aí. Ela influencia em algo?” Simmmm. Quanto maior a temperatura, maior a p s a t e aí menor o NPSHD. A temperatura também vai ter uma certa influencia em ρ e V , mas é menor e, de qualquer maneira, o enunciado diz “as demais variáveis envolvidas permaneceram inalteradas”.

O que temos que ver agora é qual era a temperatura às 10   h . Em todas as horas que a temperatura for maior do que esta, pode ter havido cavitação pois N P S H D < N P S H R , em tese. Falo “pode ter havido” porque as temperaturas informadas não são do fluido em si e sim a temperatura ambiente; embora tubulação e bomba estejam expostas à temperatura ambiente, não podemos afirmar com certeza que as temperaturas são as mesmas, certo?

Passo 3

Olhando a tabela:

T   @ 10   h = 34 ℃

Agora repara que às 12h e às 14h, a temperatura marcada foi maior que 34°C. Depois das 10   h , em que sabemos que N P S H D = N P S H R e até às 16   h , em que a temperatura ambiente é novamente igual a 34 ℃ , pode ter havido cavitação. Daí a resposta é:

  1. pode ter operado sob cavitação entre 10 h e 16 h.

Resposta

  1. pode ter operado sob cavitação entre 10 h e 16 h.

Exercícios de Livros Relacionados

Um modelo reduzido de bomba de 200m m , fornecendo água a 82° C a 50,5l / s e 2.400r p m começa a cavitar quando a pressão de entrada e a velocidade forem 82,7k P a absoluta e 6,1m / s , respectivamen
A bomba de 28p o l de diâmetro da Figura 11.7a a 1.170r p m é utilizada para bombear água a 20° C através de um sistema de tubulação a 833,3l / s . (a) Determine a potência de eixo necessária. O fator
A bomba do Problema P11.28 é redimensionada para um rotor de 18p o l , operando em água no ponto de melhor rendimento a 1.760r p m . A NPSH obtida experimentalmente é de 4,9m , e a perda por atrito en
PA11.4 – O sistema da Figura PA11.4 é projetado para fornecer água a 20 °C de um reservatório ao nível do mar para um outro através de um tubo de ferro fundido de 38 cm de diâmetro. As perdas localiza