Em determinada indústria, a bomba centrífuga X será substituída pela Y que, sabe-se de antemão, vai operar com uma vazão maior que a de X. Designando a carga positiva de sucção disponível das bombas X e Y por, respectivamente, CPSX e CPSY, considerando que o regime de escoamento com a bomba X era plenamente turbulento e mantidas inalteradas as demais variáveis envolvidas, a razão CPSY/CPSX é:
Dado: A carga positiva de sucção (CPS) corresponde ao termo da língua inglesa Net Positive Suction Head (NPSH).
Passo 1
“Nossaaaa, uma questão de concurso! Como vou fazer isso?!” Calmaaaaaaa. Bora lá que você consegue.
Temos uma bomba X e vamos substituir por uma Y. Com Y, a vazão é maior do que com a X e o enunciado pergunta a relação entre as cargas positivas de sucção disponíveis, isto é:
Como o regime é turbulento, e vale aquela equação que chegamos na teoria pra NPSHD:
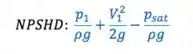
Passo 2
Quando aumentamos a vazão, mantendo as demais variáveis constantes, o que inclui a área de escoamento (isto é, diâmetro do tubo constante), a velocidade aumenta.
Por outro lado, aumentado , diminui. Aí a gente tem que estudar os dois fenômenos e decidir qual é mais importante, pra saber qual o efeito global de sobre o . A verdade é que cai muito mais do que aumenta, pois eleva-se muito as perdas de carga antes da tubulação de sucção.
Isto é, globalmente :
E vimos isso na teoria, inclusive graficamente:

Agora pensa comigo: se Y está com vazão maior do que X:
Daí:
Fechou!