Como achar o mínimo da função com ?
Passo 1
O enunciado nos dá uma função e pede para encontrarmos o mínimo dela usando a função de otimização do MATLAB .
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter muito claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a função dada no enunciado: queremos encontrar o valor mínimo de . Logo, a função é a função objetivo do problema de otimização.
A função do enunciado depende de . Logo, a variável de projeto é .
Em outras palavras, queremos encontrar o valor de que dê o menor possível.
Passo 2
Antes de partir para o MATLAB, vamos relembrar como é a função :
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
A primeira coisa que vamos fazer é entrar no MATLAB a função dada no enunciado. Em um script novo, crie uma função contendo a equação :

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada a variável , que é a variável de projeto do problema de otimização. A saída de é a variável , que é o que queremos minimizar.
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:
![]()
Na primeira linha, entramos com o “chute” inicial da variável , armazenado na variável . Escolhi , mas você pode adotar outro valor.
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .
A saída de é a variável com o valor de que dá o menor possível.
Vamos rodar o programa para ver o que o vai retornar:
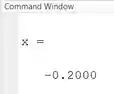
O valor de que dá o menor possível na função é .
Passo 3
Para ver qual é o valor mínimo de , acrescente no código o comando:
![]()
Com este comando, calculamos usando a função , tendo como entrada a saída de .
Rodando o programa, temos:

Logo, o menor valor possível de na função é , obtido quando .
Passo 4
Uma coisa legal de ver é se o mínimo encontrado pelo é o mesmo mínimo que encontramos quando procuramos o ponto de mínimo no gráfico da função.
Para entendermos o motivo, vamos plotar o gráfico de
Em um novo script, para plotar , digite as linhas de código:
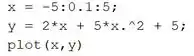
Na primeira linha, criamos um vetor que vai de a , com um passo de . Esse vetor vai ser o eixo horizontal do gráfico.
Na segunda linha, calculamos para cada elemento do vetor e armazenamos os resultados no vetor . O vetor será o eixo vertical do gráfico.
Na terceira linha, o gráfico de é gerado.
Executando o programa, temos o gráfico de :

Podemos encontrar no gráfico as coordenadas do ponto mínimo da função, clicando nele (como na figura acima). Veja que são exatamente e , dando o mesmo resultado de .
Resposta
As coordenadas do mínimo da função é e .