Considere o mecanismo de dois pares de barras, mostrado abaixo:

Os elos e têm o mesmo comprimento e os elos e têm o mesmo comprimento . A junta é uma junta fixa, e as juntas e são conexões por pino em duas corrediças que se movem sem atrito ao longo de uma linha horizontal. O mecanismo é submetido a três forças externas. Elas são as forças verticais e nas juntas e , respectivamente, e uma força horizontal na junta . Assume-se que as barras estavam alinhadas e esticadas ao longo de uma linha horizontal antes da aplicação das cargas. Também se assume que o peso do mecanismo é desprezível. O equilíbrio do mecanismo submetido às cargas aplicadas é obtido minimizando a função de energia potencial:

1. Plote a superfície e as curvas de nível da função;
2. Use com ponto inicial radianos para encontrar a energia potencial mínima.

Vamos começar pela letra a. Em um novo script, entre as constantes listadas no passo 1:

Perceba que converti as forças de para , multiplicando-as por .

Em seguida, vamos criar dois vetores, e , representando uma faixa de valores que e podem assumir:

Os vetores e vão de a , com um passo de . Eles servirão para criar os eixos X e Y dos gráficos da superfície e das curvas de nível pedidos na letra a.

Para podermos usar as funções e do MATLAB, devemos criar matrizes a partir dos vetores e , as quais contêm as coordenadas dos vetores. Faremos isso usando a função :

A função pega os vetores e , que têm elementos, e cria duas matrizes quadradas e , de tamanho . Cada linha da matriz é o vetor , repetido vezes. Já cada coluna da matriz é o vetor , também repetido vezes.

A função serve para auxiliar na criação de gráficos em três dimensões. A matriz será o eixo X do gráfico da superfície e das curvas de nível da função . Já a matriz será o eixo Y.

O eixo Z dos gráficos será a energia potencial. Por isso temos que criar uma matriz de tamanho com os resultados de para cada elemento das matrizes e . Digite no MATLAB a equação da energia potencial dada pelo enunciado, substituindo e pelas matrizes e :

Perceba que usei os três pontos (...) para quebrar a linha de código em duas, para que a equação da energia potencial coubesse toda no meu script, sem ter que usar uma barra de rolagem para vê-la por inteiro.

Após ter criado as matrizes , e , podemos gerar os gráficos pedidos na letra a. Vamos começar com a superfície da função , que será gerada usando a função do MATLAB. A função tem a sintaxe:

A plota uma superfície tridimensional com as curvas de nível abaixo dela. Ela gera um gráfico 3D com os valores da matriz no eixo X, da matriz no eixo Y e da matriz no eixo Z.

Para gerar a superfície da função , adicione no script as seguintes linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico da superfície em uma janela diferente do gráfico das curvas de nível.

Na segunda linha, o comando cria a superfície da energia potencial, tendo no eixo X, no eixo Y e no eixo Z.

Na terceira linha, o comando interpola as cores do gráfico, de forma que a superfície fica sem a malha, tendo um gradiente de cores bem bonito. Você vai ver mais pra baixo, quando gerarmos o gráfico.

Na quarta linha, o comando faz com que o gráfico tenha uma barra de cores indicando a intensidade da energia potencial.

Na quinta linha, dizemos que o eixo X do gráfico corresponde à variável de projeto , com o comando .

Na sexta linha, dizemos que o eixo Y do gráfico corresponde à variável de projeto , com o comando .

Finalmente, na última linha, indicamos que o eixo Z do gráfico corresponde à energia potencial, com o comando .

Colocamos a barra na frente de e para que apareçam as letras gregas e no eixo do gráfico.

Vamos executar o programa pra ver essa superfície:

Repare que logo abaixo da superfície, no plano , temos as curvas de nível da superfície.

Podemos ver as coordenadas dos pontos da superfície clicando neles. O ponto com menor que encontrei tem coordenadas , e . Contudo, eu não tenho certeza se esse realmente é o ponto de mínimo, pois é difícil encontrar o ponto exato de mínimo olhando só a superfície.

Vamos gerar as curvas de nível em um gráfico separado para ver se facilita.

Para gerar um gráfico de curvas de nível, usaremos a função , que tem a seguinte estrutura:

Esse comando cria um gráfico de curvas de nível, onde as isolinhas (linhas que ligam pontos de mesmo valor) correspondem aos valores da matriz . As matrizes e definem o eixo X e o eixo Y do gráfico de curvas de nível.

Para criar o gráfico de curvas de nível, digite no seu script os comandos:

Na primeira linha, pedimos ao MATLAB para criar uma segunda figura com o comando , para que o gráfico de curvas de nível seja gerado em uma janela diferente da janela onde foi plotada a superfície, no passo 3.

Na segunda linha, o comando cria o gráfico das curvas de nível da energia potencial, tendo no eixo X, no eixo Y e dando os valores para as isolinhas. As strings no final do comando () pedem ao MATLAB para mostrar o valor de cada curva do gráfico.

Na terceira linha, indicamos que o eixo X do gráfico corresponde a , com o comando . Já na quarta linha, dizemos que o eixo Y do gráfico corresponde a , com o comando .

Bora rodar o programa pra ver as curvas de nível:

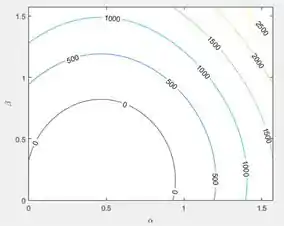
Note que é o mesmo desenho que temos no plano no gráfico da superfície, do passo 3.

Repare que as curvas com menor estão na parte inferior do gráfico. A curva de menor intensidade mostrada no gráfico é Isto significa que os ângulos e que dão o mínimo estão no interior dessa curva e que a energia potencial mínima é pelo menos , mas pode assumir valores menores ainda.

Podemos ver as coordenadas de certos pontos ao clicar sobre o ponto no gráfico. No gráfico acima, o ponto com menor que encontrei tem coordenadas , , que dão um .

Encontrei dois pontos com coordenadas muito próximas em cada gráfico, mas mesmo assim é muito difícil definir o mínimo de uma função olhando somente as figuras. A análise dos gráficos serve apenas para termos uma noção de onde se localiza o ponto de mínimo. Na minha busca, com certeza deixei passar algum ponto com energia potencial menor.

Por isso, vamos usar o para encontrar o ponto de mínimo de maneira mais precisa (e responder à letra b do exercício). O tem a sintaxe:

Precisamos fornecer a ele no mínimo duas entradas:

• uma função representando a função objetivo;
• um vetor contendo um “chute” inicial das variáveis de projeto.

A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.

Vamos criar uma nova função no MATLAB para representar a função objetivo . Abra um script novo e digite:

Chamei a função que contém a função objetivo de , mas você pode chamar do que quiser. tem como entrada o vetor , que tem dois elementos contendo as variáveis de projeto do problema de otimização: e . O primeiro elemento do vetor representa e o segundo, . A saída de é a variável , que é a energia potencial que queremos minimizar.

Repare que tive que entrar novamente com as constantes da função , listadas no passo 1.

Após criar um script com a função objetivo, vamos implementar o . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das variáveis de projeto e , armazenado no vetor . O enunciado pediu para adotarmos .

Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível de , partindo de .

A saída de é o vetor , de dois elementos, com os valores de e que dão o menor possível.

A terceira linha calcula o valor de usando a função , tendo como entrada o vetor dado por . Desta forma, encontramos a energia potencial mínima.

Vamos executar o programa e ver qual o ponto de mínimo que o nos dá:

Encontramos que a energia potencial mínima é e ela ocorre em e . Até que deu um resultado bem pertinho dos valores que tiramos dos gráficos =D