A função
Tem dois mínimos no intervalo . Encontre os valores de e de cada mínimo.
Passo 1
O enunciado nos dá uma função e diz que ela tem dois mínimos em um dado intervalo. Neste exercício, a função objetivo é e a variável de projeto é .
Para encontrarmos as coordenadas de cada mínimo da função, usaremos a função de otimização do MATLAB , variando o “chute inicial” do algoritmo.
Para termos uma noção de cada chute inicial, temos que plotar primeiro.
Passo 2
Em um novo script, digite as linhas de código abaixo par plotar :

Na primeira linha, criamos um vetor que vai de a , com um passo de . Esse vetor representa o intervalo dado pelo enunciado e vai ser o eixo horizontal do gráfico.
Na segunda linha, calculamos para cada elemento do vetor e armazenamos os resultados no vetor . O vetor será o eixo vertical do gráfico.
Na terceira linha, o gráfico de é gerado. Executae o programa para vê-lo:
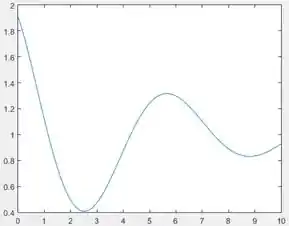
Passo 3
No gráfico de , podemos identificar os dois pontos de mínimo que o enunciado falou. Podemos achar mais ou menos suas coordenadas clicando na curva do gráfico:

Achar mínimos por gráficos é bom para se ter uma estimativa, mas se quisermos um resultado mais preciso, devemos usar algum algoritmo de otimização, que normalmente exigem um ponto de partida (ou “chute inicial”) para minimizar uma função.
Podemos escolher nossos “chutes iniciais” a partir do gráfico, por proximidade dos pontos que marcamos.
Passo 4
A função tem a sintaxe:
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um número representando um “chute” inicial da variável de projeto.
A saída de é uma variável contendo o valor da variável de projeto que minimiza a função objetivo.
Primeiramente, vamos definir a função objetivo que usaremos em usando o comando:
![]()
A função objetivo será armazenada em . O indica que é em função de , a nossa variável de projeto (não confundir com o vetor que criamos no passo 2).
Para encontrar o primeiro ponto de mínimo, o mais à esquerda, vamos adotar um “chute inicial” de :

O resultado de para é armazenado em , que é a coordenada do primeiro mínimo. A coordenada do primeiro mínimo é calculada entrando em e é armazenada em .
Temos que as coordenadas do primeiro ponto de mínimo são:

Para encontrar o segundo ponto de mínimo, vamos fazer o mesmo procedimento. Adote um “chute inicial” de :
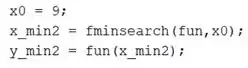
O resultado de para é armazenado em , que é a coordenada do segundo mínimo. A coordenada do segundo mínimo é calculada entrando em e é armazenada em .
Temos que as coordenadas do segundo ponto de mínimo são:

Resposta
As coordenadas do primeiro ponto de mínimo são e
As coordenadas do segundo ponto de mínimo são e