Dados os pontos experimentais:
![]()
Ajuste os coeficientes () de uma reta () aos dados experimentais.
Passo 1
O enunciado nos dá alguns pontos experimentais e pede para encontrarmos uma equação da reta que corresponda aos dados. Para isto, faremos o que chamamos de “ajuste de dados” para encontrar os coeficientes e da reta.
Normalmente, quando temos pontos com coordenadas , para encontrarmos o polinômio de grau que melhor represente esse conjunto de pontos, minimizamos o erro quadrático médio :
Para o exercício, como queremos ajustar uma reta tendo pontos, temos e o erro quadrático médio torna-se:
Para ajustar a reta aos pontos, precisamos minimizar , logo, trata-se de um problema de otimização. Vamos identificar a função objetivo e as variáveis de projeto:
- “O que eu quero minimizar?”: queremos minimizar o erro quadrático médio , logo, a função objetivo é:
- “O que eu quero minimizar depende de quê?”: depende dos pontos experimentais, dados pelo enunciado, e dos coeficientes e , que são desconhecidos e queremos determinar de forma que o erro seja mínimo. Logo, as variáveis de projeto são os coeficientes da reta e .
Resumindo, queremos encontrar os coeficientes da reta que resultem em uma reta o mais próxima possível dos dados experimentais. Para encontrar esses coeficientes usaremos a função , pois precisamos minimizar o erro quadrático médio para determinar a equação da reta.
Passo 2
Antes de partir para o MATLAB, vamos relembrar como é a função :
Precisamos fornecer a ela no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
Vamos começar criando a função representando a função objetivo. Em um novo script do MATLAB, crie uma função com dois vetores, e , contendo os dados experimentais:

Eu chamei a função de , mas você pode chamar como quiser. Ela tem como entrada um vetor de dois elementos chamado , representando as variáveis de projeto (os coeficientes e ), e como saída a variável , que será o erro quadrático médio, que queremos minimizar.
Abaixo dos vetores x e y, entre com a função objetivo. Digite as seguintes linhas de código:
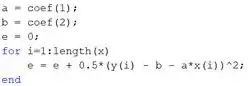
Na primeira linha, dizemos que o primeiro elemento do vetor é a variável , representando o coeficiente que multiplica o na equação da reta , isto é, o coeficiente angular.
Na segunda linha, dizemos que o segundo elemento do vetor é a variável , representando o coeficiente que está sozinho na equação da reta , isto é, o coeficiente linear.
Na terceira linha, criamos uma variável . Ela vai armazenar o erro quadrático médio, que queremos minimizar. Como o erro quadrático é calculado usando um somatório, usamos um laço para implementá-lo no MATLAB.
A partir da quarta linha, temos o laço para entrarmos com a função objetivo. Na quarta linha, inicia-se o laço , definindo uma variável de controle que vai de ao número de elementos do vetor (que é e é calculado usando a função , que retorna o número de elementos de um vetor).
Na quinta linha, calculamos o erro quadrático . A variável é atualizada a cada iteração, somando o valor obtido na iteração atual com o valor obtido na iteração anterior. Por isso temos na quinta linha e tivemos que definir antes do laço , para não termos problemas com a primeira iteração ().
Na sexta linha, encerra-se o laço .
No final, a função ficou assim:

Passo 3
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:
![]()
Na primeira linha, entramos com o “chute” inicial do vetor , armazenado na variável . Escolhi , mas você pode adotar outros valores.
Na segunda linha, usamos . Para indicar a função objetivo em , usamos o nome da função criada com a função objetivo com um na frente. Por isso a primeira entrada de , neste caso, é (caso tenha dado um nome diferente, não esqueça de trocar!). O algoritmo de otimização por trás de vai procurar o mínimo da função objetivo, isto é, o menor valor possível do erro quadrático médio , partindo de .
A saída de é vetor com os coeficientes da reta e que dão o menor erro possível.
Vamos rodar o programa e ver o que o retorna pra gente:

Temos que os coeficientes da reta que dão o melhor ajuste para os pontos experimentais são e .
Passo 4
Uma forma legal de visualizar o resultado é plotarmos a reta com os coeficientes encontrados junto com os dados experimentais.
No script do MATLAB onde você implemetou o , digite as linhas de código.
![]()
Nas duas primeiras linhas, entramos com os dados experimentais dados no enunciado, em forma de vetores.
Na terceira linha, usando o vetor , calculamos os valores de usando a equação da reta com os coeficientes dados pelo . O resultado é armazenado no vetor .
Em seguida, adicione o comando:
![]()
Ele gera um gráfico dos dados experimentais junto com a reta obtida a partir da otimização. O primeiro conjunto pede ao MATLAB para plotar o vetor em função do vetor (os dados experimentais), representando os pontos por bolinhas. O segundo par plota a reta obtida a partir da otimização.
Executando o programa, temos:
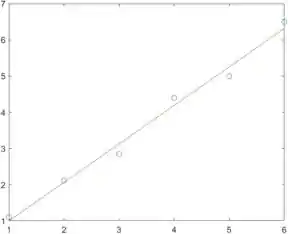
Note como a reta e os dados experimentais estão bem próximos, indicando que a nossa otimização funcionou.
Resposta
Os coeficientes da reta que dão o melhor ajuste para os pontos experimentais são e .