A figura abaixo mostra um sistema de molas em posição não-deformada sem cargas (linha tracejada) e em posição deformada com cargas nas juntas entre as molas (linha cheia.)
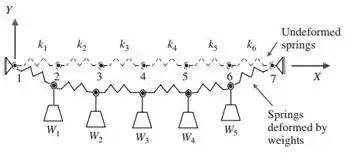
A rigidez da mola é e é definida por:
Onde é o número de cargas. O peso é definido por
O comprimento de cada mola antes da aplicação das cargas é . As coordenadas das juntas das molas (pontos ) são representadas por dez variáveis de projeto: , . Para encontrar a posição de equilíbrio, a seguinte função de energia potencial é minimizada:
Onde
Determine as posições de equilíbrio usando fminsearch, isto é, as posições das juntas para o sistema com as molas deformadas. Use o ponto inicial .
Passo 1
O enunciado nos dá uma função e pede para que encontremos o mínimo dela usando .
A primeira coisa que devemos entender bem antes de atacar o exercício é qual é o problema de otimização. Para isto, devemos ter bem claro:
- “O que eu quero minimizar?”, definindo a função objetivo;
- “O que eu quero minimizar depende do quê?”, definindo as variáveis de projeto.
O que queremos minimizar é a energia potencial do sistema de molas, representada pela função dada no enunciado:
Logo, a energia potencial do sistema é minha função objetivo.
A função objetivo depende das coordenadas das juntas das molas e de algumas constantes, como o número de cargas e o comprimento das molas relaxadas, dadas pelo enunciado:
As coordenadas das juntas a são as variáveis de projeto. Em outras palavras, queremos encontrar qual a posição das juntas a que dê a menor energia potencial possível.
Passo 2
Para vermos por onde vamos começar o exercício, vamos relembrar a sintaxe de :
A função precisa de no mínimo duas entradas:
- uma função representando a função objetivo;
- um vetor contendo um “chute” inicial das variáveis de projeto.
A saída de é um vetor contendo os valores das variáveis de projeto que minimizam a função objetivo.
O vetor nos foi dado no enunciado, falta definirmos a função objetivo dada pelo enunciado no MATLAB. Vamos começar fazendo isso. Em um script novo, crie uma função chamada (ou dê o nome que você quiser), que tem como entrada um vetor de elementos, representando as variáveis de projeto.
Entre com as constantes listadas no passo 1: o número de cargas e o comprimento das molas :

Existe outra informação que podemos tirar do enunciado, principalmente da imagem: as coordenadas das juntas e . Ambas as juntas são fixas, logo, suas coordenadas não vão mudar com a adição das cargas.
Repare que o sistema de referência está bem em cima da junta na figura do enunciado, logo, as coordenadas da junta são:
Para a junta , ela se encontra exatamente sobre o eixo do sistema de referência , logo, . Já a sua coordenada em é determinada pelo comprimento das molas sem carga: entre a junta e a junta , existem molas, logo .
Digite as coordenadas das juntas e na função :

Passo 3
Tendo as coordenadas das juntas e , vamos criar dois vetores, um com as coordenadas em das juntas do sistema, e outro com a coordenada , para nos ajudarem a construir a função objetivo. Esses vetores seriam assim:
Para criar esses vetores na nossa função, vamos usar as coordenadas , , e definidas no passo anterior e o vetor , que é a entrada da função que contém as variáveis de projeto, que são as coordenadas das juntas a . O vetor é assim:
Logo, para gerar os vetor e no MATLAB, vamos usar essas duas linhas de código:
![]()
Na primeira linha de código, o primeiro elemento do vetor é , que é seguido da primeira metade de , isto é, das coordenadas em das juntas a . O último elemento de é .
Da mesma forma, na segunda linha de código, o primeiro elemento do vetor é , que é seguido da segunda metade de , isto é, das coordenadas em das juntas a . O último elemento de é .
Passo 4
Com os vetores e definidos, podemos começar a entrar com a função obejtivo:
Vamos dividir em duas partes: o primeiro somatório se refere à energia potencial elástica e o segundo, à energia potencial gravitacional. Vamos calcular cada parte separadamente e no final, as juntamos para termos .
Vamos começar pelo primeiro somatório:
Para construi-lo, vamos precisar de um laço , para calcular e para cada e somar o produto ao produto obtido com valores de anteriores. Por isso, adicione em sua função as linhas de código:

Na primeira linha de código, criamos uma variável e a fazemos igual a . É ela quem vai representar o resultado do somatório .
Na segunda linha, inicia-se o laço , com uma variável de controle que vai de a (como no somatório da energia potencial elástica).
Na terceira e na quarta linha, calculamos a rigidez e a deformação da mola . Note que usamos os vetores e criados no passo anterior para calcular , pois a deformação depende das coordenadas das juntas.
Na quinta linha, atualizamos a variável , fazendo-a igual à soma dela mesma com o produto . Desta forma, somamos ao valor de da iteração anterior, para no final, com , termos o resultado do somatório .
Passo 5
Tendo concluído a criação do primeiro somatório, vamos partir para o segundo, o da energia potencial gravitacional:
Para construi-lo, também usaremos um laço , para calcular para cada , multiplicá-lo pela coordenada da junta e somar o produto ao produto obtido com valores de anteriores. Por isso, adicione em sua função as linhas de código:

Na primeira linha de código, criamos uma variável e a fazemos igual a . É ela quem vai representar o resultado do somatório .
Na segunda linha, inicia-se o laço , com uma variável de controle que vai de a (como no somatório da energia potencial gravitacional).
Na terceira, calculamos o peso .
Na quarta linha, atualizamos a variável , fazendo-a igual à soma dela mesma com o produto . Desta forma, somamos . ao valor de da iteração anterior, para no final, com , termos o resultado do somatório .
Note que aqui usamos o vetor criado no passo 3, pois a energia potencial gravitacional depende da posição das cargas.
Após os dois laços , podemos calcular , a nossa função objetivo:
![]()
No final, a função ficou assim:

Passo 6
Após criar um script com a função objetivo, vamos implementar a . Em um novo script, salvo na mesma pasta onde está o script da função , digite as linhas de código:

Na primeira linha, entramos com o “chute” inicial das coordenadas das juntas, armazenado no vetor , fornecido pelo enunciado.
Na segunda linha, definimos uma variável por meio de , uma função que serve para mudar alguns parâmetros do algoritmo de otimização. Nesta linha, aumentamos o número de vezes que é calculado por meio da função , alterando o parâmetro . Por padrão, o MATLAB calcula a função objetivo vezes o número de variáveis de projeto (que no nosso caso é , logo, seria vezes). Contudo, esse valor não é o suficiente para o algoritmo achar um ponto de mínimo, por isso, aumentei para vezes.
O número máximo de iterações do algoritmo também foi aumentado, mexendo no parâmetro . Por padrão, o número máximo de iterações também é vezes o número de variáveis de projeto, o que também não foi o suficiente para encontrar um ponto de mínimo. Por isso, aumentei para .
Na terceira linha, usamos . Note que dessa vez ela tem três entradas: a função objetivo, o “chute” inicial e , que é a variável criada para mexer em alguns parâmetros do algoritmo de otimização. A saída de é o vetor com as posições das juntas a que dão o menor possível.
Vamos rodar o programa para ver o que o vai retornar:
![]()
Para ver qual é o valor mínimo de , acrescente no código o comando:
![]()
Com este comando, calculamos usando a função , tendo como entrada o resultado de .
Execute o programa para ver o mínimo:
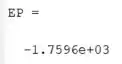
Resposta
As posições de equilíbrio das juntas para o sistema de molas é:
A energia potencial para essas coordenads é .