Em um circuito de tratamento de minérios, há uma seção de peneiramento com reciclo. A fração não passante na peneira é reciclada ao circuito, após passar por um britador, conforme o esquema abaixo:
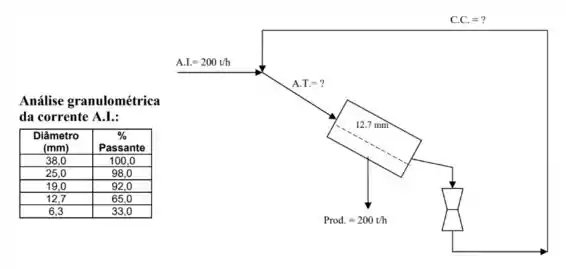
Sabendo-se que o britador fornece de material abaixo de , pede-se a vazão mássica das correntes de Carga Circulante (C.C.) e de Alimentação Total (A.T.) em .
Passo 1
Essa questão é praticamente um balanço de massa, mas envolve conceitos de peneiração também. Bora entender melhor o esquema:
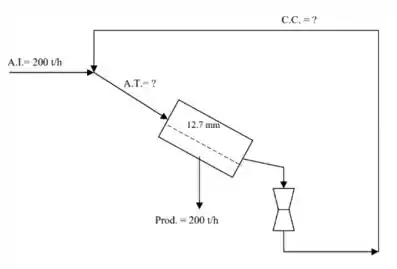
Tem uma corrente que passa por uma peneira de abertura ; parte dessa corrente consegue passar pela peneira dando origem a corrente “”, ou seja, possui diâmetro menor que . O que não passa pela peneira vai para um britador que transforma da corrente que ele recebe em um material abaixo de 12,7 mm, ou seja, da corrente que chega no britador vai conseguir passar pela peneira quando passar pela segunda vez.
O problema também dá, como dado, uma tabela com diâmetros e porcentagem passante (que é a mesma ideia do ) REFERENTE À CORRENTE ! Por exemplo, da corrente passa por uma peneira com abertura de (que é justamente o que nos interessa nesse problema haha.
Passo 2
Concorda comigo que a corrente é a soma das correntes e ? Sabemos que a corrente tem uma vazão de mas não sabemos nada sobre a vazão da ainda, então, bora dizer que tem uma vazão .
Dessa forma, a vazão de vai ser:
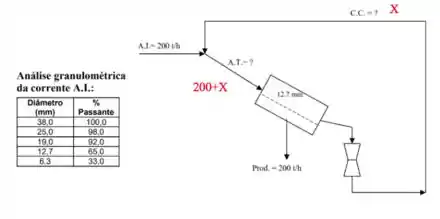
Isso que acabamos de fazer foi um balanço de massa para Mas, agora, vamos considerar apenas a fração menor que . Vou colocar um junto ao nome da corrente quanto estiver me referindo a massa dessa corrente menor que .
Quanto a , que é a corrente que sai do britador, nos foi informado que dela tem diâmetro menor que . Daí:
Daí o balanço de massa para partículas abaixo de na corrente fica:
Mas repara que a corrente é a parte da corrente que passa pela peneira, que é justamente (a corrente possui de partículas abaixo de ). Daí podemos igualar essas duas correntes:
Calculando :
E substituindo isso no balanço de massa da corrente :