Deseja-se peneirar areia, a uma vazão de , no sistema de peneiras vibratórias, segundo esquema abaixo. Determinar a produção de A, B e C, em toneladas por dia.
Supor que as peneiras são equipamentos ideais de separação.
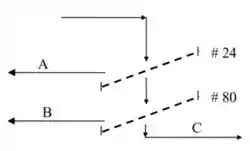
Distribuição granulométrica:

Passo 1
Vamos começar entendendo o que significa aquele esquema ali:
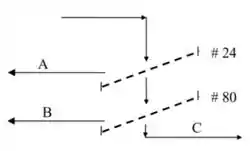
Aquela seta lááá em cima, é a areia entrando pra separação por peneiras. Aí ela cai em uma peneira de 24 Mesh. Tá vendo que tem uma parte que segue pra baixo e outra (A) que sai pelo lado? A fração A tem diâmetro maior do que o da peneira 24 Mesh, então não conseguiu passar por ela. Já os grãozinhos menores de areia, passaram pelo Mesh 24 e agora vão passar por uma segunda peneira, de Mesh 80. Mais uma vez, uma parte passa pela peneira (corrente C, formada pelos menores grãozinhos), enquanto uma outra parte fica retira, formando a corrente B.
Então os grãozinhos da corrente A são maiores que os grãozinhos da corrente B que são maiores que os grãozinhos da corrente C.
E repara que ali na tabela a gente tem muito mais peneiras. Isso porque alguém pegou uma amostra dessa areia, levou para o laboratório e fez um teste com uma cacetada de peneiras pra fazer aquela tabela com a distribuição de tamanhos, que a gente vai utilizar aqui, ok?
Passo 2
Agora que entendemos o problema, vamos começar a brincadeira.
Para esse tipo de problema, nem precisamos dos diâmetros; só com essa designação já dá pra resolver, porque não estamos interessados em tamanhos e sim nas frações dessas que vão para A, B e C.
Opa! Falamos em frações? Bora calcular os porque vamos precisar haha
Calculando :
Daí, para o primeiro intervalo (), por exemplo:
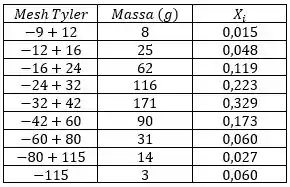
Passo 3
Agora repara que tudo que tiver ou menor (o que significa que a partícula é maior, já que é o número de aberturas por polegada linear), ficará retido na primeira peneira e, aí, irá para a corrente . O que for maior que (ou seja, partículas menores), passará por essa primeira peneira (simbolizado por ). Vou destacar, em azul, na tabela, a parte que corresponde à corrente .
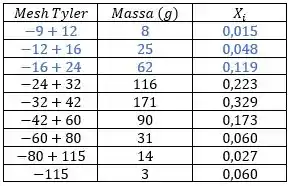
O que passa pela peneira de (simbolizado por ) mas fica retido na peneira de (simbolizado por ), vai para a corrente . Vou destacar, na tabela, em verde, a parte correspondente a corrente :
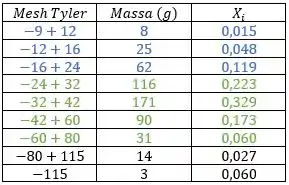
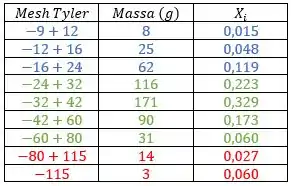
Por fim, o que passa pela peneira de vai para a corrente . Vou representar em vermelho.
Passo 4
Já dividimos a tabela e sabemos quais frações vão para quais correntes. Agora é só somar as frações parciais para achar a fração total de cada corrente e multiplicar pela vazão, que é . Assim, olha:
Daí a vazão da corrente , que vou chamar de , vai ser:
Da mesma forma:
Quanto a :
Só pra confirmar podemos verificar que a soma dessas correntes dá mesmo as 100 toneladas por dia: