(Adaptada) Trocadores de calor consistem frequentemente em muitas passagens triangulares. Uma passagem é mostrada na figura, com e seção transversal em formato de um triângulo isósceles de comprimento lateral e ângulo . Se a velocidade média é e o fluido é óleo SAE 10 a 20°C, calcule a perda de carga global.
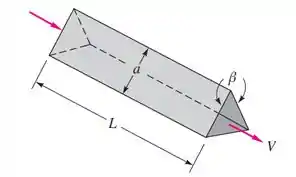
Dados: ,
Passo 1
Esse é um exercício de duto não-circular. Por isso, vamos precisar do diâmetro hidráulico para fazer os cálculos de Reynolds. Com o Reynolds descobrimos se o escoamento é laminar ou turbulento. Então vamos lá,
A área da seção do duto é a área do triângulo isósceles. Sabemos o lado a e o ângulo entre os lados iguais, então é conveniente usar essa fórmula de área do triângulo
No triângulo isósceles, a = b
Como a = 2 cm = 0,02 m e β = 80°
Show! Para calcular o perímetro molhado vamos considerar que o fluido escoa ao longo de todo o perímetro. Logo, o perímetro molhado será o próprio perímetro.
Podemos levar isso em consideração, pois o enunciado não informa se o fluido estaria ocupando apenas uma parte do duto. Beleza?
Conhecemos dois lados do triângulo, mas falta conhecer o terceiro. Para isso, vamos usar a lei dos cossenos
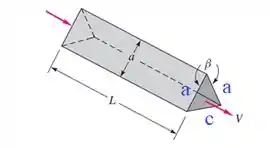
No triângulo da figura
Substituindo
Calculando o perímetro molhado
Voltando ao Diâmetro hidráulico
Passo 2
Opa! Com esse diâmetro hidráulico, vamos calcular Reynolds! :DD
Substituindo
Como Re é menor que 2300, o escoamento é laminar. Por isso, vamos usar a tabela que relaciona o fator de atrito e Reynolds no escoamento laminar a depender da geometria (nosso caso é triangular)
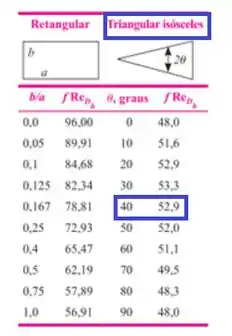
Por que selecionar o ? Pois nessa tabela, o ângulo entre os lados iguais é . Então
Pela tabela vemos que:
E assim podemos calcular a perda de carga global 😊