Em um trecho de 30 m de comprimento e 50 mm de diâmetro de uma tubulação de ferro galvanizado, água escoa e passa por uma válvula gaveta totalmente aberta, 2 cotovelos de 90° normal e um cotovelo de 45° normal também. Considerando que os acidentes são rosqueados e vazão é de , calcule a perda de carga localizada.
Passo 1
Bom dia, boa tarde, boa noite ou boa madrugada! xD Vamos começar a resolver os exercícios de Perdas Localizadas :D
Vimos na teoria que a perda localizada é o somatório de todas as perdas causadas por acidentes (obstáculos) no trecho analisado. Dá uma olhada:
Sendo o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
No nosso caso, todos os acidentes estão acontecendo numa tubulação de diâmetro 50 mm. A partir daí conseguimos calcular a velocidade e ela será a mesma para todo mundo. Podemos coloca-la para fora o somatório
Precisamos de duas coisas para calcular a perda de carga então: calcular a velocidade e descobrir os coeficientes dos acidentes! Primeiro vamos calcular a velocidade pela vazão volumétrica
A área é a área de um tubo circular de diâmetro 50 mm, ou seja, 0,05 metros. Sempre bom usar o Sistema Internacional (SI)! Aliás, a vazão também precisa ser convertida para o SI.
Com isso achamos a velocidade na tubulação
Passo 2
Agora vamos encontrar os coeficientes de perda localizada. Os acidentes são:
- 1 válvula gaveta totalmente aberta
- 2 cotovelos de 90° normal
- 1 cotovelo de 45° normal
Lembrando que são rosqueados e o diâmetro é de 50 mm, hein! Vamos ver isso na tabela
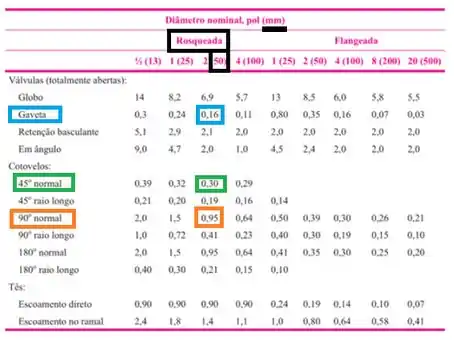
Assim, pela tabela encontramos que
Calculando a perda localizada
Detalhe importante! Multiplicamos o K do cotovelo de 90° por 2, pois temos esse mesmo acidente 2 vezes. Os outros não foram multiplicados porque só tem 1 de cada. Fechado?
Vamos as contas. Substituindo
Perda localizada calculada! =D