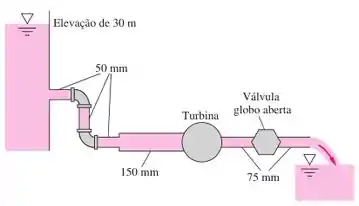
Na Figura encontram-se de tubo de , de tubo de e de tubo de , todos de ferro fundido. Há também 3 cotovelos de e uma válvula globo aberta, todos flangeados. Se a elevação de saída é zero, qual é a potência em extraída pela turbina quando a vazão é de de água a ?
Formulário:
-Contração Brusca:
-Expansão Brusca:
Passo 1
Nesta questão devemos mais uma vez montar a equação da energia:
Repare que temos dois somatórios:
-Das perdas globais
-Das perdas locais
-Além da energia que a turbina precisa
Nos próximos passos listaremos cada uma das perdas que vamos calcular.
As condições de entrada são:
Na saída:
Logo a equação fica com a seguinte cara:
Rearranjando em função da turbina:
Passo 2
Como já conhecemos e , vamos listar e calcular as perdas globais, existem três pois temos três variações de diâmetro na tubulação:
é do tubo de com diâmetro ;
é do tubo de com diâmetro ;
é do tubo de com diâmetro .
Comecemos pela primeira perda :
Calcularemos a velocidade e então o número de Reynolds, sendo e :
Dado que a rugosidade do tubo é
Logo, pelo Diagrama de Moody,
Substituindo na expressão da perda de carga:
Fazendo o mesmo para as outras duas perdas de carga:
Para a terceira:
Somando todas as três perdas:
Passo 3
Agora vamos listas as perdas locais:
- Na entrada da tubulação, contração brusca;
- 3 cotovelos de normal;
- 1 válvula globo aberta;
- Na saída, expansão brusca.
Na contração:
Se :
Nos cotovelos, olhamos valores tabelados:
Na válvula, também pegamos valores tabelados:
Na expansão brusca:
Logo nosso somatório fica:
Passo 4
Lembrando da expressão que deduzimos no primeiro passo, iremos substituir as variáveis que não conhecíamos:
Logo a potência da turbina em é igual a :