Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Perdas localizadas e Dutos não-circulares

Ver Teoria
Exercício 21345678

Enunciado

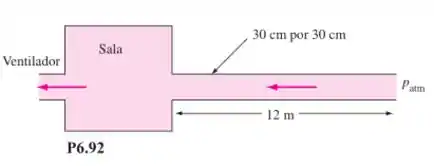
Uma grande sala usa um ventilador para succionar o ar atmosférico a 20 ℃ por um duto de aço comercial de 30   c m por 30   c m por 12   m de comprimento, como na Figura P6.92. Calcule a pressão na sala, se a vazão for 1200   m ² / h . Despreze as perdas localizadas.

Passo 1

Neste exercício devemos estamos considerando um duto não circular! É um duto de seção quadrada.

Antes de calcularmos o diâmetro hidráulico, vamos como sempre olhar a equação da energia. Vamos considerar que nosso volume de controle começa no início do duto e termina na entrada da sala.

Tanto a velocidade, quanto a altura não muda de um ponto a outro do duto, logo a equação fica com a seguinte cara:

p 1 - p 2 ρ g = h p = f L D h V ² 2 g

Passo 2

Vamos calcular o número de Reynolds para sabermos o tipo de regime em que estamos:

Calculamos o diâmetro hidráulico D h :

D h = 4 A P m = 4 × 30 × 30 30 + 30 + 30 + 30

D h = 30   c m

Se a velocidade é

As propriedades do ar são ρ = 1,2   k g / m ³ e μ = 1,8 × 10 - 5 k g / ( m . s )

Se a velocidade é V = Q / A

V = 1200 ÷ 3600 30 × 10 - 2 ² = 3,70   m / s

Logo R e D h :

R e D h = ρ V D h μ = 1,2 × 3,70 × 0,30 1,8 × 10 - 5

R e D h = 74000

Regime turbulento, podemos usar o Diagrama de Moody como aproximação.

Passo 3

Sabemos que o material é aço comercial, logo:

ϵ = 0,046   m m

ϵ D h = 0,046 × 10 - 3 0,30

ϵ D h = 0,000153

No Diagrama de Moody:

f ≈ 0,02

Passo 4

Substituindo na expressão inicial da equação da energia:

p 1 - p 2 ρ g = f L D h V ² 2 g

Como queremos p 2 :

p s a l a = p a t m - ρ f L D h V ² 2

Neste caso vamos usar a escala absoluta de pressão:

p a t m = 1   a t m = 10 5   P a

Substituindo todos valores, temos a expressão:

p s a l a = 10 5 - 1,2 × 0,02 12 0,3 3,70 ² 2

p s a l a = 99993   P a

Resposta

p s a l a = 99993   P a

Exercícios de Livros Relacionados

Quando lidamos com a lubrificação de rolamentos, a equação de governo que descreve a pressão é a equação de Reynolds, geralmente descrita em uma dimensão como: d d x h 3 μ . d p d x + 6 U . d h d x =
Uma grande massa é suportada por um pistão de diâmetro D = 100m m e comprimento L = 100m m . O pistão está assentado em um cilindro fechado no fundo. A folga a = 0,025m m entre a parede do cilindro e
A distribuição de velocidade em uma fina película de fluido escoando para baixo sobre uma superfície inclinada foi desenvolvida no Exemplo 5.9. Considere um filme de 7 mm de espessura de um líquido co
Um mancal de deslizamento selado é formado por cilindros concêntricos. O raio interno e o externo são 25 e 26 mm, respectivamente, o comprimento do mancal é 100 mm, e ele gira a 2800 rpm. A folga radi
O perfil de velocidade para escoamento completamente desenvolvido de óleo castor a 20 °C entre placas paralelas em movimento, é dado pela Eq. 8.8. Considere U = 1,5m / s e a = 5m m . Determine o gradi