Calcular a porosidade de um leito fluidizado formado pela adição de de catalisador () em uma coluna com de diâmetro, sabendo-se que a altura do leito, nas condições de fluidização, é igual a .
Passo 1
Temos um leito fluidizado com as seguintes dimensões:
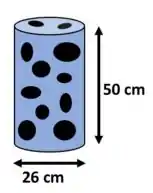
O enunciado diz que tem de catalisador, que são as nossas partículas, nesse leito. A densidade das partículas é dada:
No resto do volume do leito vai ter fluido. Esse fluido está preenchendo o volume de “vazio”, que é onde não tem partículas.
O exercício pede pra calcular a porosidade (), então bora lembrar a fórmula dela:
Passo 2
Bora calcular esse volume total () logo:
Como tanto como estão em , a unidade do volume vai ser :
Passo 3
Já resolvemos o termo do denominador da porosidade. Falta agora o numerador: “volume de vazio”.
Mas olha só: o volume de vazio é a parte do volume total em que NÃO tem partículas, certo? Então, escrevendo isso:
Lembra que esse subscrito “” no é como eu estou indicando que estamos falando de partículas.
Daí, posso reescrever a fórmula de porosidade:
Repara que já fizemos coisa parecida em exercícios anteriores, mas neles eu calculei o volume de vazio separado e depois que joguei na fórmula. Aqui, eu já estou jogando o cálculo do dentro da fórmula de porosidade. Mas dá no mesmo.
Passo 4
Tá, já temos o então só falta o para acharmos a porosidade. Mas temos a massa de partículas ( e a densidade delas (), daí calculamos o :
Rearranjando:
Agora muita calma nessa hora, padawan! Repara que a massa de partículas () que temos está em , mas a unidade de massa da densidade está em . Precisamos escolher uma das duas para converter e eu vou escolher não o Pikachu, mas sim o .
Convertendo o :
Cortando os “” e colocando em notação científica:
Agora, com unidades compatíveis, podemos calcular o :
Daí:
Passo 5
Agora é só substituir tudo na fórmula de porosidade que achamos:
Os nossos volumes estão na mesma unidade, , então não precisamos converter nada:
ou
Resposta
ou