Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 8

Suponha que as variáveis aleatoriamente X, Y e Z tenham a seguinte distribuição de probabilidades conjuntas

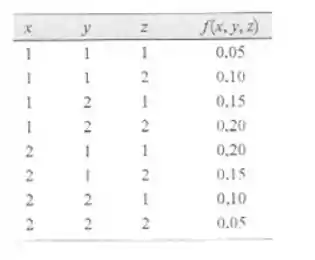
Determine o seguinte:

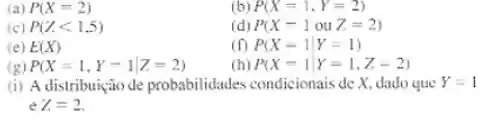
Passo 1

Temos a distribuição de probabilidade conjunta para X, Y e Z dada na tabela.

R X = R Y = R Z = { 1,2 }

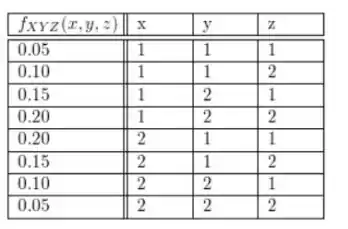
Passo 2

Letra a:

Precisamos encontrar a probabilidade P ( X = 2 ) . Lembre-se que nós calculamos a distribuição marginal pela definição:

P ( X = x ) = ∑ y ∈ R Y ∑ x ∈ R Z P ( X = x ,   Y = y ,   Z = z )

Que significa que:

P ( X = 2 ) = f X Y Z ( 2,1 , 1 ) + f X Y Z ( 2,1 , 2 ) + f X Y Z ( 2,2 , 1 ) + f X Y Z ( 2,2 , 2 ) = 0.5

onde f X Y Z ( 2 , y , z ) = 0 para todos os outros valores y , z ∈ { 1,2 }

Passo 3

Letra b:

Também a partir da distribuição marginal (pode ser facilmente comprovado), obtemos:

P ( X = x ,   Y = y ) = ∑ x ∈ R Z P ( X = x ,   Y = y ,   Z = z )

ou o que nós realmente precisamos, que é:

P ( X = 1 ,   Y = 2 ) = f X Y Z ( 1,2 , 1 ) + f X Y Z ( 1,2 , 2 ) = 0.35

Passo 4

Letra c:

Aqui, procuramos a seguinte probabilidade:

P ( Z < 1.5 ) = ∑ x ∈ R x ∑ y ∈ R y P ( Z < 1.5 , X = x ,   Y = y )

P ( Z < 1.5 ) = ∑ x ∈ R x ∑ y ∈ R y P ( Z = 1 , X = x ,   Y = y )

= f X Y Z ( 1,1 , 1 ) + f X Y Z ( 1,2 , 1 ) + f X Y Z ( 2,1 , 1 ) + f X Y Z ( 2,2 , 1 ) = 0.5

Os únicos valores possíveis para Z

Passo 5

Letra d:

Podemos olhar para o evento { A   o u   B } como um evento { A   ∪ B } . Usando P ( A ∪ B ) = P ( A ) + P ( B ) - P ( A , B ) que representa qualquer evento A e B, obtemos:

P ( X = 1   o u   Z = 2 ) = P ( { X = 1 } ∪ { Z = 2 } ) = P ( X = 1 ) + P ( Z = 2 ) - P ( X = 1 , Z = 2 )

onde calculamos as probabilidades da mesma forma que fizemos acima, então obtemos:

P ( X = 1   o u   Z = 2 ) = 0.5 + 0.5 - 0.3 = 0.7

Passo 6

Letra e:

A expectativa matemática da variável aleatória discreta X é a soma do produto de cada possibilidade x com sua probabilidade P ( X = x ) :

E ( X ) = ∑ x P ( X = x )

Já calculamos P ( X = 1 ) = 0.5 e P ( X = 2 ) = 0.5 , então:

E ( X ) = 1 × 0.5 + 2 × 0.5 = 1.5

Passo 7

Letra f:

Da definição de probabilidade condicional, temos:

P ( A | B ) = P ( A , B ) P ( B )

onde estão A e B são eventos, e P ( B ) > 0 .

O que significa que:

P ( X = 1 | Y = 1 ) = P ( X = 1 ,   Y = 1 ) P ( Y = 1 ) = 0.3

Passo 8

Letra g:

O mesmo que acima, nós calculamos:

P ( X = 1 ,   Y = 1 | Z = 2 ) = P ( X = 1 ,   Y = 1 ,   Z = 2 ) P ( Z = 2 ) = 0.2

Passo 9

Letra h:

E essa letra h é igual à questão acima também:

P ( X = 1 ,   Y = 1 | Z = 2 ) = P ( X = 1 ,   Y = 1 ,   Z = 2 ) P ( Y = 1 ,   Z = 2 ) = 0.4

Passo 10

Letra i:

Quando aplicamos probabilidade condicional (pode ser comprovada), nós temos:

f X | Y = 1 ,   Z = 2 ( x ) = f X Y Z ( x , 1,2 ) f Y Z ( 1,2 )

a partir do qual calculamos o que precisamos, para x = 1 e x = 2

f X | Y = 1 ,   Z = 2 ( 1 ) = f X Y Z ( 1,1 , 2 ) f Y Z ( 1,2 ) = 0.4

f X | Y = 1 ,   Z = 2 ( 2 ) = f X Y Z ( 2,1 , 2 ) f Y Z ( 1,2 ) = 0.6

Resposta

  1. P ( X = 2 ) = 0.5
  2. P ( X = 1 ,   Y = 2 ) = 0.35
  3. P ( Z < 1.5 ) = 0.5
  4. P ( X = 1   o u   Z = 2 ) = 0.7
  5. E ( X ) = 1.5
  6. P ( X = 1 | Y = 1 ) = 0.3
  7. P ( X = 1 , Y = 1 | Z = 2 ) = 0.2
  8. P ( X = 1 | Y = 1 ,   Z = 2 ) = 0.4
  9. f X | Y = 1 ,   Z = 2 ( 1 ) = 0.4

f X | Y = 1 ,   Z = 2 ( 2 ) = 0.6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Referindo-se ao Exercício 3.39, determine(a) f( y| 2 ) para todos os valores de y.(b) P( Y = 0 |X = 2) .
Considere X e Y vida útil, em anos, de dois componentes em um sistema eletrônico. Se a função de densidade conjunta dessas variáveis é f x , y = e - ( x + y ) , x0 , y0 0 ,c a s oc o n t r á r i o á D
Se a distribuição de probabilidade conjunta de X e Y é dada por f x , y = x + y 30 ,x = 0 ,1 ,2 ,3 ; y = 0 ,1 ,2 , Determine(a) P ( X ≤ 2 ,Y = 1 ) ;(b) P ( X2 ,Y ≤ 1 ) ;(c) P ( XY ) ;(d) P X + Y = 4 .
Considere um experimento que consiste em duas jogadas de um dado balanceado. Se X é o número de resultados quatro e Y é o número de resultados cinco obtidos em duas jogadas do dado, determine(a) a dis
Suponha que X e Y tenham a seguinte distribuição de probabilidade conjunta:(a) Determine a distribuição marginal de X.(b) Determine a distribuição marginal de Y.