Na transmissão de informação digital, a probabilidade de se ter um bit com alta, moderada e baixa distorção é de 0.01,0.04,0.95, respectivamente. Suponha que três bits sejam transmitidos e que a intensidade de distorção de cada bit seja considerada independente. Sejam X e Y os dois números de bits com distorção alto e moderada, respectivamente, dos três transmitidos. Determine o seguinte:
- qual é a probabilidade de dois bits terem distorção alga e um ter distorção moderada?
- Qual é a probabilidade e todos os três bits terem distorção baixa?
- A distribuição de probabilidades, a média e a variância de X.
- A distribuição de probabilidades condicionais, a média condicional e a variância condicional de X, dado que Y=2.
Passo 1
Temos distorção alta (evento H), moderada (evento M) e baixa (evento L).
Seja:
e a quantidade de distorção de cada bit é considerada independente. Sejam X e Y o número de bits com distorção alta e moderada dentro dos três, respectivamente.
Temos que a função de massa seguirá uma distribuição multinomial
De três acertos, escolhemos x para estar com alta distorção e y com moderado e o resto são distorções baixas, isso significa que podemos calcular probabilidades acima assim.
Ao multiplicar as probabilidades, obtemos para cada . Após o cálculo nós temos:
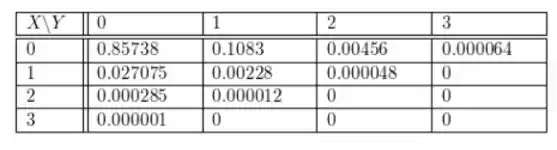
Não é possível obter 2 com distorção alta e 2 com distorção moderada de 3 bits. Mesma explicação para os outros zeros.
Passo 2
Letra a:
Para dois bits com alta distorção, definimos e para uma distorção moderada, definimos y = 1, obtemos da tabela.
Passo 3
Letra b:
A probabilidade de que todos os três tenham baixa distorção é para e que é na verdade da tabela.
Passo 4
Letra c:
Calculamos a distribuição marginal por definição:
O que significa que é uma soma das probabilidades em cada linha, ou podemos escrever como:

A expectativa matemática da variável aleatória discreta X é a soma do produto de cada possibilidade x com sua probabilidade
Usando a definição, obtemos:
é a variÂncia da variável aleatória X, definida como:
Para calcular , observe que é uma variável aleatória discreta e que pode ser escrito como nós sabemos que:
Usando isso, temos:
E agora, temos:
Passo 5
Letra d:
Da definição de probabilidade condicional temos:
onde A e B são eventos, e . Nós podemos usá-lo para a função de massa também, então temos:
Onde sabemos que (soma da segunda coluna), e todos os valores de para todo . Calculando o quociente, obtemos a distribuição, ou a função de massa:

Demos as definições acima, então vamos usá-las:
Note que você pode notar que as probabilidades de distribuições não somam 1. isso é por causa dos cálculos! Além disso, existem muitas aproximações, então pode ser correto usar em vez de = , isso requer muito tempo para calculá-lo e existem algumas aproximações bem conhecidas de Distribuição Binomial/Distribuição Multinomial!
Resposta
- Ver resolução
- 0.85738
- Ver resolução,
- Ver resolução,