Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 27
10-27. A distância global viajada por uma bola de golfe é testada. ati-
rando a bola com o lron Byron,um jogador mecânico.com um balanco
que é dito emular o legendario campe:io Byron Nelson. Dez bolas, sele-
cionadas alcatoriamente a partir de duas marcas diferentes, são testa-
das, sendo a distáncia global medida. O)s dados são:
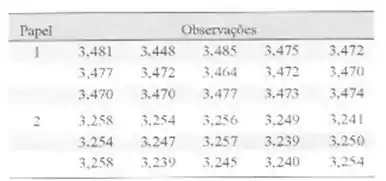
a) Há evidencia de que a distância global seja distribuída aproximada-
mente de forma normal? Uma suposição de variâncias iguais é
justificada?
b) Teste a hipótese de que ambas as marcas de bola tém iguais distân
cias médias globais. Use a = 0.05. Qual é o valor P?
c)Construa um intervalo de confiança de 955 para a diferença média
entre as duas marcas de bolas de golfe.
d) Qual é a potência do teste estatístico do item (b) para detectar uma
diterenca verdadeira na distancia média global de 5 jardas?
e) Que tamanho de amostra seria requerido para detectar uma diferen-
ça verdadeira na distáncia média global de 3 jardas com poténcia de
aproximadamente 0.75?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
Marca 1:
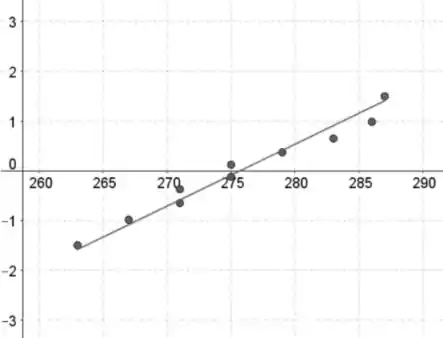
Marca 2:
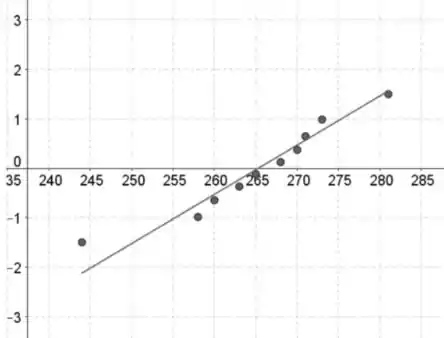
A suposição de normalidade parece válida. É provável que os padrões nos gráficos de probabilidade normal sejam aproximadamente lineares e não contenham nenhuma curvatura forte.
A suposição de variâncias iguais parece ser válida, porque a razão dos desvios padrão (maior para o menor) é menor que 2.
Passo 3
Letra b:
Determine as hipóteses:
Determine o desvio padrão agrupado:
Determine a estatística de teste:
Determine o valor P correspondente da tabela de distribuição T-Student no apêndice com :
Se o valor P for menor ou igual ao nível de significância, então a hipótese nula é rejeitada:
Há evidências suficientes para apoiar a alegação de que os mesmos da população são diferentes.
Passo 4
Letra c:
Determine usando a tabela de distribuição T-Student, que é dada na coluna com e na linha com:
Determine o desvio padrão agrupado:
Os pontos finais do intervalo de confiança para são:
Estamos confiantes de que a distância geral média da marca 1 é entre e mais alta do que a distância total média da marca 2.
Passo 5
Letra d:
diferença média hipotética
diferença média verdadeira
Determine o desvio padrão agrupado:
O fator de escala de abscissas d é o valor absoluto da diferença absoluta nas diferenças médias dividido por duas vezes o desvio padrão da população.
Então, obtemos a probabilidade de um erro do tipo II usando as curvas características operacionais no apêndice para com e :
A potência é 1 diminuída da probabilidade de um erro de II:
Passo 6
Letra e:
Diferença média hipotética
Diferença média verdadeira
Potência
Determine o desvio padrão agrupado:
O fator de escala de abscissas d é o valor absoluto da diferença absoluta nas diferenças médias dividido por duas vezes o desvio padrão da população.
Em seguida, obtemos o tamanho da amostra usando as curvas características de operação no apêndice para com e :
O tamanho da amostra n é o valor obtido a partir das curvas características de operação acrescidas de 1, dividido por 2.
Resposta
- Suposição satisfeita
- . Há evidências suficientes para apoiar a alegação de que os mesmos da população são diferentes.