Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 30
10-30. Considere os dados de estacionamento no Excmplo 10-10.
a) Use o teste temparelhado para investigar a afirmaçào de que os dois
tipos de carros tem diterentes níveis de dificuldade para estacionar
de forma paralela. Usc = 0.10.
b) Compare seus resultados com o intervalo de confianca construido
no Exemplo 10-10 e comente por que eles são os mesimos ou por
que eles são diferenles.
c) Investigue a suposição de que as diferencas nos lempos para estacio-
nar sejam normalmente distribuidas.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Do exemplo 10-10 sabemos que a média da amostra e o desvio padrão das diferenças são
Letra a:
Nós consideramos o teste de hipótese
Contra
O teste estatístico é:
Como
concluímos isso no nível de confiança de 90%, os dados não apoiam a afirmação de que os dois carros têm diferentes níveis de dificuldades de estacionamento e .
Agora, da Tabela V do Apêndice, sabemos
Então, os limites superior e inferior para o valor P são
Porque , falhamos em rejeitar .
Passo 2
Letra b:
Do Exemplo 10-10 sabemos que o intervalo de confiança de para um intervalo de confiança de é
Observe que o intervalo de confiança em inclui zero. Isso implica a mesma conclusão que na parte a), como era de se esperar.
Passo 3
Letra c:
A suposição de normalidade parece razoável para ambas as amostras que verificaremos com base no gráfico de probabilidade normal.
Um gráfico de probabilidade normal é um método gráfico para determinar se os dados da amostra estão em conformidade com uma distribuição normal hipotética com base em um exame visual subjetivo dos dados.
Para construir um gráfico de probabilidade, as observações na amostra são primeiro classificadas do menor ao maior. Ou seja, a amostra é organizado como onde é a menor observação, é a segunda menor observação, e assim por diante com o maior. A frequência cumulativa para observação é
Uma probabilidade normal é construída em eixos ordinários traçando as pontuações normais padronizadas contra onde as pontuações normais padronizadas satisfazem
Nos eixos horizontais estão os valores . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados se desviarem significativamente de uma linha reta, o modelo hipotético não é apropriado.
Passo 4
Da maneira descrita anteriormente, nós construímos um gráfico de probabilidade normal. com base em observações 19.2 5.6 -0.6 47.2 0.6 -5 7 26 5.8 1.2 -6.2 0.6 4 -24 é
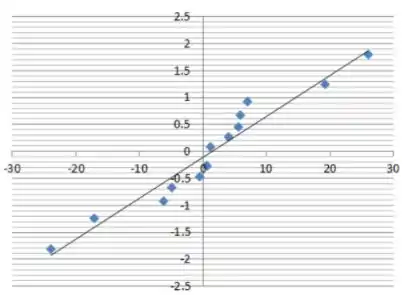
Os gráficos de probabilidade normal não contêm curvatura forte, então eles indicam que há uma suposição correta sobre a suposição de normalidade.
Resposta
- Como . Falhamos em rejeitar . Os limites superior e inferior para o valor P são .
- Observe que o intervalo de confiança em cima inclui zero. Isso implica a mesma conclusão que na parte a).
- Os gráficos de probabilidade normal não contêm curvatura forte, então, eles indicam que há uma suposição correta sobre a suposição de normalidade.