Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 34
10-34. Um artigo no Journal of Aircrafi (Vol. 23. 1986. p. 859 864
desereve uma nova formulaçào do método de análise de placa equiva.
lente, que é capaz de modclar estruturas de aviocs. tais comks vigas-cal
xão nas asas de avióes, e que produz resultados similares ao método de
análise por elementos finitos. que é mais laborioso computacionalmen-
te. Freqüencias naturais de vibração para a estrutura das vigas caixao nas
asas de aviões são calculadas usando ambos os métodos, sendo os resul-
tados mostrados a seguir para as sete primeiras frequencias naturais.
a) Os dados sugerem que os dois métodos fornecem o mesmo valor
médio para a freqüência natural de vibração? Use a = 0,05. Encon-
tre o valor P.
b) Encontre um intervalo de confianca de 95% para a diferenca média
entre os dois métoxdos.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Determine a diferença no valor de cada par.
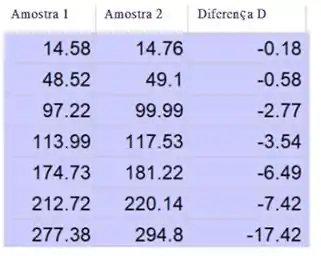
Passo 2
Letra a:
Determine as hipóteses:
Determine a média da amostra das diferenças:
Determine o desvio padrão da amostra das diferenças:
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor que o nível de significância, rejeita a hipótese nula.
Há evidências suficientes para rejeitar a alegação de que os dois métodos fornecem o mesmo valor médio para a frequência de vibração natural.
Passo 3
Letra b:
Determine o usando a tabela V com
Os limites inferiores do intervalo de confiança são então:
Resposta
- . Há evidências suficientes para rejeitar a afirmação de que os métodos fornecem o mesmo valor médio para a frequência de vibração natural.