Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 38
10-38. Em Biomctrics(1990. Vol. 46. pp.673-87).os autores analisa-
ram a circunferencia de cinco laranjeiras (marcada como A-E), medi-
das em sete cxasioes (x).
a)Comparc o aumento medio na circunferéneia nas periodos l a 2 com
o aumento medio para os periodos 2 a 3. O aumento é a ditrenca na
circunferéneia nes dois periodos. Essas médias são signifieativamen
te diferentes com a - 0,10?
b) Há evidência de quc o aumento mélio no perindo 1 a 2 seja maior
do que o aumenio medio no periodo 6 a 7 coma =0.05?
c) As suposiçòes do teste do item ta) são violadas porque os mesmos
dados (cireunterencia do periodo 2, são usaclos para calcular ambos
osaumentos medios?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Determine a diferença no valor de cada par.
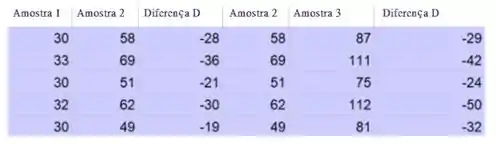
Passo 2
Letra a:
Determine a média da amostra das diferenças:
Determine o desvio padrão da amostra das diferenças:
Determine as hipóteses:
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o número inteiro mais próximo):
O valor P é a probabilidade de obtenção do valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor que o nível de significância, rejeita a hipótese nula.
Não há evidências suficiente para apoiar a afirmação de que os meios são diferentes.
Passo 3
Letra b:
Determine a diferença de valor de cada par.
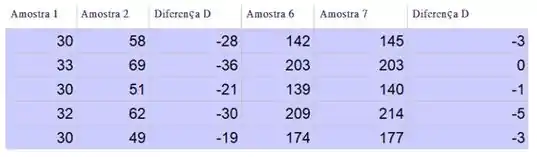
Determine a média da amostra das diferenças (a primeira média e o desvio padrão da amostra são os mesmos da parte (a)):
Determine o desvio padrão da amostra das diferenças:
Determine as hipóteses:
Determine a estatística de teste:
Determine os graus de liberdade (arredondados para o número inteiro mais próximo):
O valor P é a probabilidade de obtenção do valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor que o nível de significância, rejeita a hipótese nula.
Há evidências suficientes para apoiar a alegação de que o aumento médio do período 1 ao período 2 é maior do que o aumento médio do período 6 ao período 7.
Passo 4
Letra c:
As premissas do teste na parte (a) são violadas, porque os dados dos dois períodos devem ser independentes
Resposta
- Não há evidência suficiente para apoiar a alegação de que os meios são diferentes.
- Há evidência suficiente para apoiar a afirmação de que o aumento médio no período 1 ao período 2 é maior do que o aumento médio no período 6 ao período 7.
- Sim