Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios Suplementares - Ex. 106

106. O artigo “Error Distribution in Navigation” (J. Institute of Navigation, 1971, p. 429-442) sugere que a distribuição de freqüência de erros positivos (magnitudes dos erros) é bem aproximada por uma distribuição exponencial. Seja X o erro de posição lateral (milhas náuticas), que pode ser negativo ou positivo. Suponha que a fdp de X seja

f x = 0,1 e - 0,2 x                 - ∞ < x < ∞

a. Desenhe um gráfico de f(x) e demonstre que f(x) é uma fdp legítima (mostre que a integral é 1).

b. Deduza a fdc de X e faça o gráfico.

c. Calcule P(X ≤ 0), P(X ≤ 2), P(-1 ≤ X ≤ 2) e a probabilidade de se cometer um erro de mais de 2 milhas.

Passo 1

Fala galerinha boa? Tudo bem com vocês? Vamos realizar mais um exercício sobre Distribuição de probabilidades.

Na letra a:

∫ - ∞ ∞ f x d x = ∫ - ∞ 0 0,1 e 0,2 x d x + ∫ 0 ∞ 0,1 e 0,2 x d x = 0,5 + 0,5 = 1

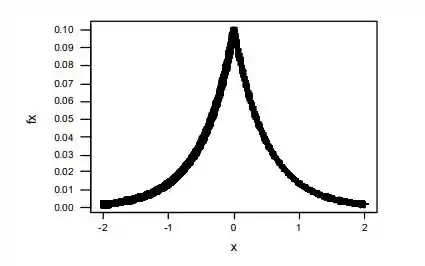
Passo 2

Na letra b, para x

F x = ∫ - ∞ x 0,1 e 0,2 y d y = 1 2 e 0,2 x

Para x ≥ 0:

F x = 1 2 + ∫ 0 x 0,1 e 0,2 y d y = 1 - 1 2 e 0,2 x

Valeu, moçada! Até a próxima!

Resposta

Nos passos anteriores.

Exercícios de Livros Relacionados

Considere uma doença cuja presença pode ser identificada por um teste sangüíneo. Sejap a probabilidade de um indivíduo selecionado aleatoriamente ter a doença. Suponha que n indivíduos sejam seleciona
Um fabricante de pilhas de lanterna deseja controlar a qualidade de seus produtos rejeitando os lotes em que a proporção de pilhas com voltagem inaceitável seja muito alta. Assim, em cada lote grande
Quarenta por cento das sementes de milho possuem espigas simples e as outras 60%, espigas duplas. Uma semente com espiga simples produzirá uma planta com espigas simples em 29% das vezes, enquanto uma
Um plano de fidelidade de viagens de executivos foi desenvolvido por uma companhia aérea sob a premissa de que 10% de seus clientes atuais se qualificariam para participar.a. Admitindo a validade dess
Uma empresa de consultoria educacional está tentando decidir se alunos de ensino médio que nunca usaram uma calculadora podem resolver um tipo de problema mais facilmente com uma calculadora que usa l