10-62. Um especiahista comprou 25 resistores de um vendedor T e 35

resistores de um vendedor 2. Cada resisténcia do resistoré medida com

os seguintes resultados:

a) Qual é a suposição necessária à distribuição de modo a testar a alir-

mação de que a variância da resistencia do produto do vendedor 1

não é significativamente diferente da variância da resistencia do

produto do vendedor 2? Faça um procedimento gráfico para veriti-

car essa suposicao.

b) Faça um procedimento estatístico apropriado de teste de hipoteses

de modo a deterninar se o especialista poxe afirmar que a variância

da resisténcia do produto do vendedor I é significativamente dife-

reute daquela do produto do vendedor 2.

Letra a:

Gráfico da probabilidade normal:

Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.

Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .

A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.

Amostra 1:

Amostra 2:

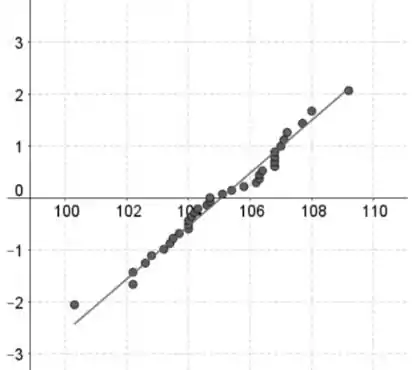
A suposição normal parece satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente normal, o que indica que as distribuições são aproximadamente distribuídas normalmente.

Letra b:

Determine as hipóteses:

Determine a estatística de teste:

O valor crítico é dado na quarta tabela da tabela VI na linha com e na coluna com :

A região de rejeição contém todos os valores menores que 0.4525 e todos os valores maiores que 2.01.

Se o valor da estatística de teste estiver na região de rejeição, em seguida, rejeite a hipótese nula:

Não há evidências suficientes para apoiar a afirmação de diferentes variações populacionais.