Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 94
8-94.Um artigo na revista Journal of Hranan Nurition and Dietetics,
＂The Validation of Energv and Protein Imtakes b Doubly laibeled Water
and 24-ffour Urinary Nitrogen Etcretion in Post-Ohese Subjects-
A Valiacao de Energiae Admissao de Proteina por Agua Duplamente
Marcada c Excrecao Urinaria de Nitrogenio em 24 Hloras em Pessoas
Pos Obesas(1995.Vol 8.pp.51-64)mostrou a energia admtida ex-
pressa como uma taxa metabolica basal(TMB),dada em MJ.
（a) Use um grafico de probabilidade normal para venficar a suposicao
de normalidade.
（b)Encontre um intervalo bilateral de confianca de 99para a media
Passo 1
Letra a:
Um gráfico de probabilidade normal é um método gráfico para determinar se os dados de amostra estão em conformidade com uma distribuição normal hipotética com base em um exame visual subjetivo dos dados. Para construir um gráfico de probabilidade, as observações na amostra são primeiro classificadas da menor para a maior. Ou seja, a amostra é organizado como onde é a menor observação, é a segunda menor observação, e assim por diante com o maior. A frequência cumulativa para observação em é:
Uma probabilidade normal é construída em eixos ordinários traçando as pontuações normais padronizadas contra onde as pontuações normais padronizadas satisfazem
Nos eixos horizontais, os valores são . Se a distribuição hipotética descreve adequadamente os dados, os pontos traçados cairão aproximadamente ao longo de uma linha reta. Se os pontos traçados desviarem significativamente da reta, o modelo hipotético não é apropriado.
Da maneira descrita anteriormente, construímos um gráfico de probabilidade normal com base nas observações 5.40 5.67 5.79 6.85 6.92 5.70 6.08 5.48 5.44 5.51
Passo 2
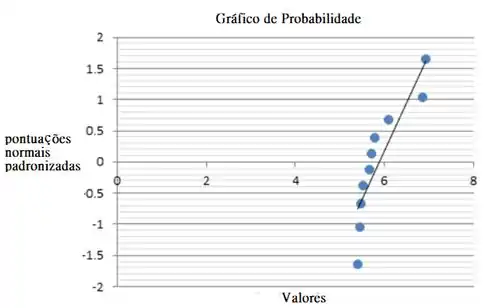
O gráfico de probabilidade normal não contém curvatura forte e o padrão é aproximadamente linear, então podemos concluir que os valores dos dados são aproximadamente normalmente distribuídos.
A média da amostra é
E o desvio padrão é:
Se e s são a média e o desvio padrão de uma amostra aleatória de uma distribuição normal com variância desconhecida , um IC de de é dado por
onde é ponto percentual superior da distribuição t com graus de liberdade.
Passo 3
Letra b:
Agora, precisamos encontrar um IC de 99% na média da população, então
Das Equações (1) e (2), obtemos
Portanto, um IC de 99% na média da população é:
Resposta
- Os valores dos dados são aproximadamente normalmente distribuídos,