Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 118
9-118. Um artigo na revista Food lesting and Analyszs (“Improving Re-
producibiliry of Refractometry Measurements of Fruit Juices" - Me-
Thorando a Reprodutibilidade de Medidas de Refratometria de Sucos de
Frulas. 1999. Vol. 4. N." 4. p 13-171 mediu a conccntracao ( Brix) de
açúcar em suco claro de maçàa. Todas as leituras foram tomadas a 20:
a) Teste a hipótese Encontre o valor P.
b)Calcule a potencia do teste se a média verdadeira for 11.4.
c) Que tamanho de amostra seria requenido para detectar uma concen-
tração média verdadeira de 11.45 se quiséssemos que a potência do
teste fosse no minimo 0.9?
d) Explique como a pergunta do item (a) poderia ser respondida cons-
truindo um intervalo de confianca bilateral para a concentração média
de açúcar.
e) Há evidencia para confirmar a suposição de que a concentracão de
açúcar seja normalmente distribuida?
Passo 1
E aiii gente, tudo bom??
Vamos começar a resolvar essa questão que é super tranquila!
Confia em mim
Dado:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Determine as hipóteses:
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor do que o nível de significância, a hipótese nula é rejeitada.
Há evidências suficientes para apoiar a afirmação de que a média é diferente de .
Passo 3
Letra b:
A potência é a probabilidade de rejeitar a hipótese nula quando a hipótese alternativa for verdadeira.
Determine o valor t correspondente a e na tabela V:
A média da amostra correspondente é a média da população (da hipótese) aumentada pelo produto do valor z e o desvio padrão:
O valor t é a média da amostra diminuída pela média da população (média alternativa). dividido pelo desvio padrão:
Determine a probabilidade de rejeitar a hipótese nula usando a tabela V.
Passo 4
Letra c:
O poder é a probabilidade de rejeitar a hipótese nula quando a hipótese alternativa for verdadeira.
Determine o valor t correspondente com e na tabela V:
Determine o valor t correspondente a e na tabela V:
A média da amostra correspondente é a média da população (da hipótese) aumentada pelo produto do valor z e o desvio padrão:
O valor t é a média da amostra diminuída pela média da população (média alternativa), dividida pelo desvio padrão:
Esses valores devem ser iguais a
Adicione 2.093 a cada lado:
Divida cada lado por 2.2624:
Eleve ao quadrado cada lado e arredonde até o inteiro mais próximo.
Existe uma outra equação que tem uma raiz real, que é que tem um tamanho de amostra de .
O tamanho mínimo da amostra é então o valor mais alto de n encontrado por qualquer equação:
Passo 5
Letra d:
Se o intervalo de confiança bilateral contém 11.5, então não há suficientes evidências para apoiar a afirmação de que a média da população é diferente de 11.5.
Se o intervalo de confiança bilateral não contém 11.5, então há evidências suficientes para apoiar a alegação de que a média da população é diferente de 11.5.
Passo 6
Letra e:
Os resultados dos dados estão no eixo horizontal e os escores normais padronizados estão no eixo vertical.
Se os dados contiverem valores de dados, as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde ao menor valor de dados, o segundo menor, a pontuação padronizada corresponde ao segundo menor valor de dados e e assim por diante.
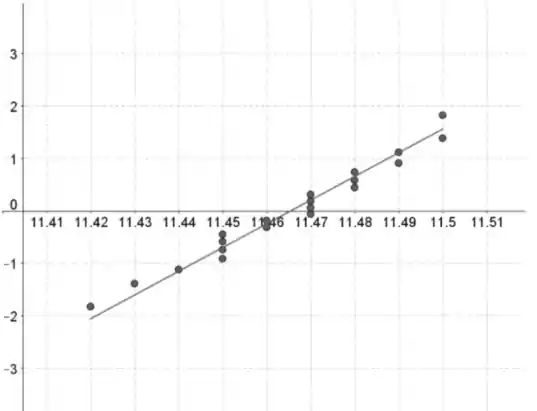
O padrão no gráfico de probabilidade normal não contém forte curvatura e parece ser aproximadamente linear. Isso indica que os dados são normalmente distribuídos.
Resposta
- Há evidências suficientes para apoiar a alegação de que a média é diferente de 11.5.
- Se o intervalo de confiança bilateral contém 11.5, então não há evidência suficiente para apoiar a alegação de que a média da população é diferente de 11.5.
- Sim
Se o intervalo de confiança bilateral não contém 11.5, então há evidências suficientes para apoiar a alegação de que a média da população é diferente de 11.5.