Numa amostra de 20 elementos de uma população normal obteve-se variância de 25. Ao nível de 10%, testar: , contra .
Passo 1
Olá galerinha, vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses.
Então primeiramente iremos definir nossa hipótese nula () e alternativa ():
- ;
- .
Pelo enunciado sabemos que , e como iremos testar a variância, iremos usar o teste qui-quadrado (), com graus de liberdade.
Para este teste temos a seguinte equação:
Onde:
- tamanho da amostra;
- variância amostral;
- valor da hipótese nula.
Passo 2
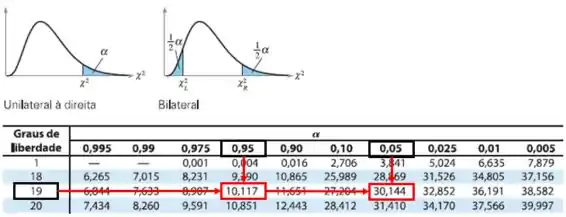
Então com os seguintes dados:
- ;
- ;
- limite superior;
- limite inferior.
E pela tabela da distribuição qui-quadrado, conseguimos definir nossa região crítica:
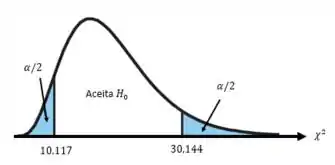
- Se ou rejeita ;
- Se aceita .
Passo 3
Então por último, conseguimos calcular o valor de e comparar com nossa região crítica, do enunciado sabemos:
- ;
- .
Logo:
Como , então aceitamos .
Tchau galerinha! Te espero em mais exercícios.
Resposta
aceita .