Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 2.Exercícios - Ex. 78

Amostras de uma peça de alumínio fundido são classificadas com base no acabamento (em micropolegadas) da superfície e nas medidas de comprimento. O resultados de 100 peças são resumidos a seguir:

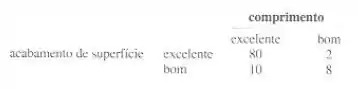
Seja A o evento em que uma peça tenha excelente acabamento na superfície e seja B o evento em que uma peça um disco tenha excelente comprimento. Determine:

  1. P ( A )
  2. P ( B )
  3. P ( A | B )
  4. P ( B | A )
  5. Se a peça selecionada tiver excelente acabamento na superfície, qual será a probabilidade do comprimento ser excelente?
  6. Se a peça selecionada tiver bom comprimento, qual será a probabilidade de que o acabamento na superfície seja excelente?

Passo 1

Letra a:

P ( A ) = 0.82

Passo 2

Letra b:

P ( B ) = 0.9

Passo 3

Letra c:

P ( A ∩ B ) = 0.8

P ( A | B ) = P ( A ∩ B ) P ( B ) = 8 9

Passo 4

Letra d:

P ( B | A ) = P ( A ∩ B ) P ( A ) = 40 41

Passo 5

Letra e:

P ( B | A ) = P ( A ∩ B ) P ( A ) = 40 41

Passo 6

Letra f:

P ( A | B ' ) = P ( A ∩ B ' ) P ( B ' )

A gente vai precisar de

P ( B ' ) = 1 - P ( B ) = 0.1

P ( A ∩ B ' ) = 2 100 = 0.02

então,

P ( A | B ' ) = 0.2

Resposta

  1. P ( A ) = 0.82
  2. P ( B ) = 0.9
  3. P ( A | B ) = P ( A ∩ B ) P ( B ) = 8 9
  4. P ( B | A ) = P ( A ∩ B ) P ( A ) = 40 41
  5. P ( B | A ) = P ( A ∩ B ) P ( A ) = 40 41
  6. P ( A | B ' ) = 0.2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que AeB sejam eventos mutuamente excludentes. Construa um diagrama de Venn que contenha os três eventos A , BeC , de modo que P ( A | C ) = 1 e P ( B | C ) = 0 .
Se cada elemento de um determinante de segunda ordem for zero ou um, qual será a probabilidade de que o valor do determinante seja positivo? (Admita que os elementos do determinante sejam escolhidos i
Sempre que um experimento é realizado, a ocorrência de um particular evento A é igual a 0,2 . O experimento é repetido independentemente, até que A ocorra. Calcule a probabilidade de que seja necessár
Demonstre que, se A e B forem eventos independentes, também o serão A e B - , A - e B , A - e B - .
Quatro sinais de rádio são emitidos sucessivamente. Se a recepção de cada um for independente da recepção de outro, e se essas probabilidades forem 0,1 ; 0,2 ; 0,3 e 0,4 , respectivamente, calcule a p