Com base em experiências anteriores, a Companhia Telefônica sabe que das contas dos seus clientes em uma comunidade são pagas com atraso. Para os itens abaixo, compare a solução exata com aquela obtida através de aproximação da variável aleatória pela distribuição normal.

1. Se 20 contas são enviadas em um dia pela Companhia Telefônica, qual é a

probabilidade de que menos do que 3 sejam pagas com atraso?

Então na letra A, vamos calcular usando a fórmula da binomial, e depois utilizando a aproximação pela normal padrão:

Então com queremos saber a probabilidade de menos de 3 cartas serem pagas com atraso; em outras palavras:

Lembra que eu disse que a gente não consegue calcular isso usando a binomial?

Então precisamos fazer aparecer uma igualdade:

Vamos ter, usando a fórmula da binomial:

OBs: busca na mémoria que:

Agora é só calcular isso daê:

Agora, vamos calcular aproximando a binomial pela normal, vamos ter o seguinte:

Onde , e não se esqueça da correção de continuidade, pois estamos aproximando uma variável discreta(binomial) por uma contínua(normal).

Tente se lembrar disso:

Ou

E

Ou

Lembrando também que usamos a normal padrão:

Perceba então, que na alternativa A teremos:

E

Então a aproximação pela normal:

Chegamos em:

Perceba que queremos:

Como cada metade do gráfico é simétrica,

Só precisamos buscar no gráfico o valor de

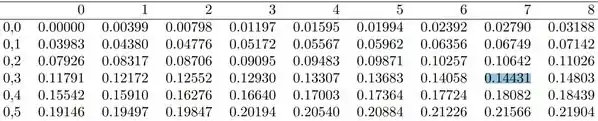
Portanto,

Então: