Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 32

Baseando-se nas projeções de preço de duas matérias primas, M 1 e M 2 , pretende-se estudar a viabilidade econômica do lançamento de um certo produto. A função conjunta de probabilidade com os preços (em reais) é apresentada a seguir:

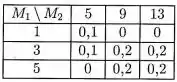
a) Determine o preço médio e a variância das matérias primas.

b) O produto usa 2 unidades de M 1 e 3 de M 2 . Qual é seu custo médio?

c) Se o produto deverá ser vendido por 50 reais, qual será o lucro médio por unidade?

Passo 1

Da distribuição conjunta, conseguimos tirar as distribuições marginais:

P M 1 = 1 = 0,1 + 0 + 0 = 0,1

P M 1 = 3 = 0,1 + 0,2 + 0,2 = 0,5

P M 1 = 5 = 0 + 0,2 + 0,2 = 0,4

Da mesma forma,

P M 2 = 5 = 0,1 + 0,1 + 0 = 0,2

P M 2 = 9 = 0 + 0,2 + 0,2 = 0,4

P M 2 = 13 = 0 + 0,2 + 0,2 = 0,4

Com isso, podemos calcular os valores médios:

E M 1 = 1 ⋅ P M 1 = 1 + 3 ⋅ P M 1 = 3 + 5 ⋅ P M 1 = 5

E M 1 = 1 ⋅ 0,1 + 3 ⋅ 0,5 + 5 ⋅ 0,4 = 3,6

Analogamente,

E M 2 = 5 ⋅ P M 2 = 5 + 9 ⋅ P M 2 = 9 + 13 ⋅ P M 2 = 13

E M 2 = 5 ⋅ 0,2 + 9 ⋅ 0,4 + 13 ⋅ 0,4 = 9,8

Passo 2

Para achar a variância, temos que

V a r M 1 = 1 - E M 1 2 P M 1 = 1 + 3 - E M 1 2 P M 1 = 3 + 5 - E M 1 2 P M 1 = 5

Logo,

V a r M 1 = - 2,6 2 ⋅ 0,1 + - 0,6 2 ⋅ 0,5 + 1,4 2 ⋅ 0,4 = 1,64

Da mesma forma,

V a r M 2 = 5 - E M 2 2 P M 2 = 5 + 9 - E M 2 2 P M 2 = 9 + 13 - E M 2 2 P M 2 = 13

Portanto,

V a r M 2 = - 4,8 2 ⋅ 0,2 + - 0,8 2 ⋅ 0,4 + 3,2 2 ⋅ 0,4 = 8,96

Passo 3

Como o produto usa 2 unidades de M 1 e 3 unidades de M 2 , temos que

p r e ç o = 2 M 1 + 3 M 2 ⇒ E p r e ç o = 2 E M 1 + 3 E ( M 2 )

Logo,

E p r e ç o = 2 ⋅ 3,6 + 3 ⋅ 9,8 = 36,6

Como ele será vendido por 50 reais, o lucro médio será

E l u c r o = 50 - E p r e ç o = 50 - 36,6 = 13,4

Resposta

E M 1 = 3,6             e           V a r M 1 = 1,64

E M 2 = 9,8             e           V a r M 2 = 8,96

E p r e ç o = 36,6

E l u c r o = 13,4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um artigo no Journal of Database Management “Experimental Study of a Self-Tuning Algorithm for DBMS Buffer Pools“ [“Estudo Experimental de um Algoritmo de Autoajuste para DBMS Buffer Pools “(2005. Vol
Uma fábrica usar dois dispositivos de inspeção para mostrar uma fração de sua saída, com objetivo de controlar a qualidade. O primeiro monitor de inspeção é capaz de detectar a cura da mente 99,3% dos
Uma classe de estatística para engenheiros tem 40 estudante, 60% de gente elétrica, 10% de engenharia industrial e 30% de engenharia mecânica. Uma amostra de quatro estudantes ser selecionado aleatori
Na transmissão de informação digital, a probabilidade de um bit ter alta, moderada e baixa distorção é 0.01, 0.04 e 0.95, respectivamente. Suponha que três bit sejam transmitidos e que a quantidade de
Na transmissão de informação digital, a probabilidade de se ter um bit com alta, moderada e baixa distorção é de 0.01,0.04,0.95, respectivamente. Suponha que três bits sejam transmitidos e que a inten