Uma fábrica usar dois dispositivos de inspeção para mostrar uma fração de sua saída, com objetivo de controlar a qualidade. O primeiro monitor de inspeção é capaz de detectar a cura da mente 99,3% dos itens defeituosos que a fábrica recebe, enquanto o segundo dispositivo é capaz de detectar 99,7% dos casos. Considere que quatro itens defeituosos são produzidos enviados para inspeção. Sejam X e Y o número de itens que serão identificados como defeituosos pelos dispositivos de inspeção um e dois, respectivamente. Suponha que os dispositivos sejam independentes. Determine

Passo 1
Letra a:
Temos dois dispositivos, onde a precisão de detecção dos itens defeituosos que ele recebe para um é 0.993 e para o segundo 0.997. Seja o evento do primeiro dispositivo que detecta com acurácia o defeito como , então e seja o evento do segundo dispositivo que detecta com acurácia o defeito como B, então .
O que significa que, e , são as probabilidades do complemento. Nós temos que os eventos A e B são independentes, porque os dispositivos são independentes.
Temos quatro itens enviados para inspeção. Sejam X e Y o número de itens que serão identificados como defeituosos pela inspeção dos dispositivos 1 e 2, respectivamente. Isso não significa necessariamente que X e Y sejam independentes.
Vamos encontrar a função de massa conjunta para as variáveis aleatórias X e Y, . Por exemplo, será a probabilidade do evento.
Passo 2
Usamos como exemplo x=2 e y=2, a explicação para outros probabilidades é a mesma. Para cada um dos quatro itens, o primeiro dispositivo verifica e, em seguida, o segundo dispositivo, o que significa que há 8 check-ins no total. Vamos ver o que é probabilidade
do evento ”ambos os dispositivos encontraram defeito nos dois primeiros itens, e que não existe nenhum defeito nos dois segundos itens ”. Podemos escrever como
Aqui usamos a independência dos eventos A e B.
Mas para o evento E acima, não estamos interessados em qual dos quatro itens tem defeito (estamos apenas interessados no número de defeitos) então o evento , também está incluído no evento E.
Vamos agora verificar qual é a probabilidade do evento T - ”o dispositivo 1 detectou os primeiros dois itens como defeituosos e outros como não defeituosos e o dispositivo 2
detectou 2 itens com defeito e 2 itens sem defeito ”. Neste caso, existem vários eventos incluídos, eles podem ser escritos como a união de todos os eventos possíveis na forma , onde é tanto B ou e apenas dois pares de dois podem ser o mesmo. Quantos eventos existem? Aqui é fácil notar que existem eventos nesta forma. Então nós temos o seguinte:
Aqui usamos quando A e B são independentes (mutuamente exclusivos), que representa qualquer combinação dos eventos.
Aqui nós também usamos independência e o que calculamos acima é o mesmo para todas as probabilidades da soma.
Passo 3
Agora, finalmente, podemos ver o que o evento E realmente é um evento. Agora não somos
interessados em qual dos quatro itens tem os defeitos, então vamos apenas somar todas as combinações, então obtemos:
Usando a mesma lógica e explicação, agora podemos criar a função de massa conjunta:
Multiplicando as probabilidades, obtemos a função de massa conjunta para
cada . Após o cálculo, nós temos:
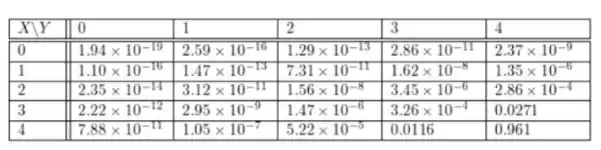
Passo 4
Letra b:
Vamos calcular a distribuição marginal pela definição:
O que significa que é uma soma das probabilidades em cada linha, podemos notar (quando
somamos as probabilidades e obtemos exatamente as mesmas probabilidades para a Distribuição binomial ou podemos notar o mesmo no exercício) que na verdade, segue a distribuição Binomial com os parâmetros e n = 4, e podemos escrever como :
O mesmo vai para
Passo 5
Letra c:
A expectativa matemática da variável aleatória discreta X é a soma do produto de cada possibilidade x com sua probabilidade
Mas é bem sabido que a expectativa de variável aleatória com distribuição Binomial é:
Passo 6
Letra d:
Da definição de probabilidade condicional temos:
onde A e B são eventos, e . Podemos usá-lo para função de massa também, então temos:
onde sabemos e todos os valores de para cada
Provamos acima que então realmente obtemos que segue a distribuição binomial com os parâmetros e
Passo 7
Letra e:
Como acima, temos distribuição binomial, então:
Passo 8
Letra f:
é a variância da variável aleatória X que segue a distribuição Binomial com os parâmetros e é . Usando isso variável aleatória , temos:
Passo 9
Letra g:
Encontramos distribuições marginais para X e Y. As verificações são as seguintes funções iguais para todos :
O que é óbvio de (a) e (b). Conclusão: eles são independentes.
Note que não podemos usar a independência antes de prová-la (por exemplo em (a)).
Resposta
- Ver resolução
- Ver resolução
- 3.972
- Ver resolução
- 3.988
- 0.0120
- Eles são independentes