Uma classe de estatística para engenheiros tem 40 estudante, 60% de gente elétrica, 10% de engenharia industrial e 30% de engenharia mecânica. Uma amostra de quatro estudantes ser selecionado aleatoriamente, sem reposição, para um grupo de projeto. Sejam X e Y o número de engenheiros industriais e mecânicos, respectivamente, determine o seguinte:

Passo 1
Distribuição hipergeométrica
N= tamanho da população = 40
n = Número de sorteios = 4
= Número de sucessos observados = 10%
Número de sucessos observados = 30%
Letra a:
Se houvesse cursos de engenharia industrial sorteados e pode haver y cursos de engenharia mecânica sorteadas, então havia engenheiros eletricistas.
Passo 2
Letra b:
Avalie a função na parte (a) para todos os valores x e y possíveis. A distribuição marginal de X é então a soma das probabilidades de todos os valores possíveis de Y (linha total).
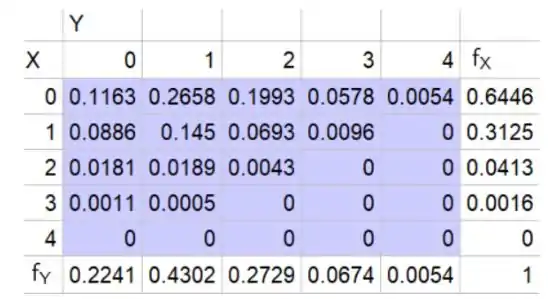
Passo 3
Letra c:
O valor esperado é a soma do produto de cada possibilidade x com sua probabilidade :
Passo 4
Letra d:
A distribuição de são os valores na linha com X = 3 da tabela dividido pelo total da linha:
Passo 5
Letra e:
O valor esperado é a soma do produto de cada possibilidade x com sua probabilidade
Passo 6
Letra f:
A variância é o valor esperado do desvio ao quadrado da média:
Passo 7
Letra g:
Não é independente, porque se houver 4 cursos de engenharia industrial X, então não pode haver especialização em engenharia mecânica então X e Y são relacionados (que significa não independente).
Resposta
- 0.6446, 0.3125, 0.0413, 0.0016, 0
- 0.3999
- 0.6875, 0.3125, 0.0413, 0.0016, 0
- 0.3125
- 0.2148
- Não é independente