Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 29

Sejam U = Y 2 e V = X + Y , com função de probabilidade conjunta entre X e Y dada na tabela a seguir

a) Obtenha a conjunta de U e V .

b) Calcule P U = 4     V = 1 ) .

c) Determine C o v U ,   V .

Passo 1

Nesse problema, o primeiro passo é montar uma tabela com os pares X ,   Y e suas respectivas probabilidades. Vou aproveitar para já computar U = Y 2 e V = X + Y nessa mesma tabela!

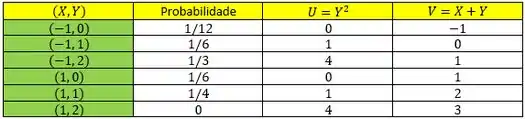
Com essa tabela de frequências, podemos construir a tabela da distribuição conjunta com as variáveis U e V :

Olhando na tabela já podemos tirar as distribuições marginais P U = u e P V = v :

P U = 0 = 1 4 ,             P U = 1 = 5 12               e             P U = 4 = 1 3

P V = - 1 = 1 12 ,         P V = 0 = 1 6 ,         P V = 1 = 1 2           e         P V = 2 = 1 4

Passo 2

No item (b), queremos calcular P U = 4     V = 1 ) :

P U = 4     V = 1 ) = P U = 4     e     V = 1 P ( V = 1 )

Da tabela, tiramos que

P U = 4     e     V = 1 = 1 3           e         P V = 1 = 1 2

Logo,

P U = 4     V = 1 ) = 1 / 3 1 / 2

Portanto,

P U = 4     V = 1 ) = 2 3

Passo 3

No item (c), queremos achar

C o v U ,   V = E U V - E U E V

Considerando a tabela de frequências:

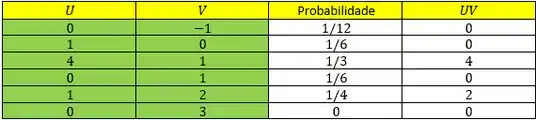
Temos que

P U V = 0 = 1 12 + 1 6 + 1 6 + 0 = 5 12

P U V = 2 = 1 4

P U V = 4 = 1 3

Assim,

E U V = 0 ⋅ P U V = 0 + 2 ⋅ P U V = 2 + 4 ⋅ P U V = 4

E U V = 0 + 2 ⋅ 1 4 + 4 ⋅ 1 3 = 11 6

Da mesma forma,

E U = 0 ⋅ P U = 0 + 1 ⋅ P U = 1 + 4 ⋅ P U = 4

E U = 0 + 1 ⋅ 5 12 + 4 ⋅ 1 3 = 21 12 = 7 4

Por fim,

E V = - 1 ⋅ P V = - 1 + 0 ⋅ P V = 0 + 1 ⋅ P V = 1 + 2 ⋅ P ( V = 2 )

E V = - 1 12 + 0 + 1 ⋅ 1 2 + 2 ⋅ 1 4 = 11 12

Portanto,

C o v U ,   V = E U V - E U E V = 11 6 - 7 4 ⋅ 11 12

Assim,

C o v U ,   V = 11 48

Resposta

P U = 4     V = 1 ) = 2 3

C o v U ,   V = 11 48

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um site da internet de pequenos negócios tem 100 páginas, em que 60%, 30% e 10% das páginas contém baixo, moderado alto conteúdo gráfico, respectivamente. Uma amostra de quatro páginas é selecionada,
Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjuntas.Determine o seguinte: f) a distribuição de probabilidade de marginais da variável aleatória X. g) A distr
Suponha que as variáveis aleatoriamente X, Y e Z tenham a seguinte distribuição de probabilidades conjuntasDetermine o seguinte:
O tempo entre os problemas de acabamento de uma superfície em um processo geral de galvanização é exponencialmente distribuído, com uma média de 40 horas. Uma única planta opera três linhas de galvani
Para a marca de referência do Conselho de desempenho do processamento de transação do exercício 5.10, sejam X, Y e Z e o número médio de operações de seleciona, atualizar e insere requerido para cada