Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 3.4 - Ex. 9

Num certo restaurante, paga-se pelo almoço uma quantia fixa dependendo da escolha feita de prato e bebida. A carne de peixe tem 10% de preferência, enquanto frango tem 40% e carne bovina 50%. As três escolhas de bebida estão condicionadas à opção do prato, segundo a tabela abaixo:

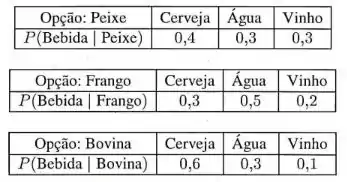
Admita os seguintes preços:

  1. Dado que alguém escolhe peixe, qual a probabilidade de que escolha cerveja?
  2. Se escolhe carne bovina, qual a probabilidade de tomar vinho?
  3. Sabendo que tomou água, qual a chance de ter escolhido frango?
  4. Determine a função de probabilidade para cada uma das variáveis X : preço do almoço e Y : preço do almoço para aqueles que preferem cerveja.

Passo 1

  1. Temos uma probabilidade condicional, então lembrando a fórmula:

    2. P B A = P A ∪ B P A

    Mas como temos a tabela Opção: Peixe, não precisamos usar a fórmula, já que a tabela já da para gente esse valor condicional:

    P C e r v e j a P e i x e = 0,4

    Passo 2

  2. Através da tabela de Opção: Bovina, podemos averiguar, que se a carne escolhida foi bovina, a probabilidade de tomar vinho é de 0,1 .

    3. Passo 3

  3. Vamos usar o teoremas de Bayes:

    4. P A B = P B A P A P ( B )

    P F r a n g o Á g u a = P Á g u a F r a n g o × P F r a n g o P Á g u a

    P F r a n g o Á g u a = 0,5 × 0,4 P ( Á g u a )

    P Á g u a = 0,1 × 0.3 + 0,4 × 0,5 + 0,5 × 0,3 = 0,03 + 0,2 + 0,15 = 0,38

    Logo:

    P F r a n g o Á g u a = 0,5 × 0,4 0,38 = 0,526

    Passo 4

  4. Antes de começar a resolução desse item, vamos calcular P ( C e r v e j a ) e P ( V i n h o ) , visto que já calculamos P ( Á g u a )

P C e r v e j a = 0,1 × 0,4 + 0,4 × 0,3 + 0,5 × 0,6 = 0,46

P V i n h o = 0,1 × 0,3 + 0,4 × 0,2 + 0,5 × 0,1 = 0,16

Existem 5 possíveis preços, logo X = { 15 ,   18 ,   21 ,   24 ,   27 }  

P X = 15 = P P e i x e × P Á g u a = 0,1 × 0,38 = 0,038

P X = 18 = P F r a n g o × P Á g u a + P P e i x e × P C e r v e j a

P X = 18 = 0,4 × 0,38 + 0,1 × 0,46 = 0,198

P X = 21 = P P e i x e × P V i n h o + P F r a n g o × P C e r v e j a + P B o v i n a × P Á g u a

P X = 21 = 0,1 × 0,16 + 0,4 × 0,46 + 0,5 × 0,38 = 0,39

P X = 24 = P F r a n g o × P V i n h o + P B o v i n a × P C e r v e j a

P X = 24 = 0,4 × 0,16 + 0,5 × 0,46 = 0,294

P X = 27 = P B o v i n a × P V i n h o = 0,5 × 0,16 = 0,08

Passo 2

Já o preço do almoço para aqueles que preferem cerveja temos Y = { 18 ,   21 ,   24 }   , vamos usar o teorema de Bayes:

P P e i x e C e r v e j a = P C e r v e j a P e i x e × P P e i x e P ( C e r v e j a ) = 0,4 × 0,1 0,46 = 0,0 9

P F r a n g o C e r v e j a = P C e r v e j a F r a n g o × P F r a n g o P ( C e r v e j a ) = 0,3 × 0,4 0,46 = 0,26

P B o v i n a C e r v e j a = P C e r v e j a B o v i n a × P B o v i n a P ( C e r v e j a ) = 0,6 × 0,5 0,46 = 0,65

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema de inspeção óptica deve distinguir diferentes tipos de peças. A probabilidade de uma classificação correta de qualquer peça é 0.98. Suponha que três peças sejam inspecionadas e que as class
Em um processo de fabricação de semicondutores, três pastilhas de um lote são testadas. Cada pastilha é classificada como passa ou falha. Suponha que a probabilidade de uma pastilha passar no teste se
Um arranjo consiste em dois componentes mecânicos. Suponha que as probabilidades do primeiro e do segundo componentes satisfazerem as especificações sejam iguais a 0.95 e 0.98. Considere que os compon
Para os Exercícios 3-15 a 3-18, verifique que as seguintes funções são funções de probabilidade e determine as probabilidade requeridas. P ( X = 2 ) P ( X ≤ 2 ) P ( X2 ) P ( X ≥ 1 )
Determine a função de distribuição cumulativa da variável aleatória do Exercício 3-22.