Cientistas e engenheiros querem comparar com freqüência duas técnicas diferentes para medir ou determinar o valor de uma variável. Em tais situações, o interesse centraliza-se em testar se a diferença média nas medições é zero. O artigo "Evaluation of the Deuterium Dilution Technique Against the Test Weighing Procedure for the Determination of Breast Milk Intake" (Amer. J. Clinical Nutr., 1983, p. 996-1003) relata os dados a seguir sobre a quantidade de leite ingerida por cada uma das 14 crianças selecionadas aleatoriamente.
a. É plausível que a distribuição da população de diferenças seja normal? b. Parece que a diferença média real entre os valores de entrada medidos pelos dois métodos é diferente de zero? Determine o valor P do teste e use-o para chegar a uma conclusão no nível de significância 0,05
Passo 1
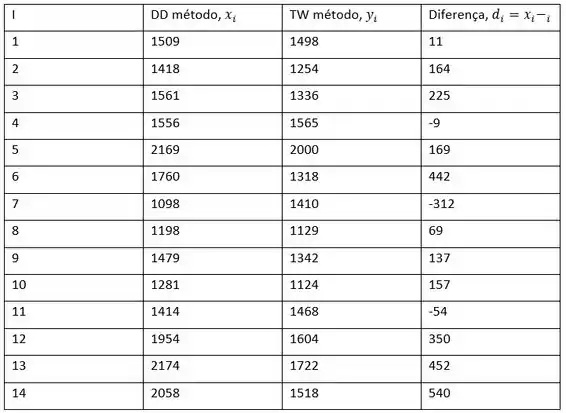
Os dados infantis são fornecidos na tabela a seguir:
- O gráfico de probabilidade normal indicou que as diferenças são normalmente distribuídas. É plausível que a distribuição populacional das diferenças seja normal
- Como o experimento foi realizado nos mesmos 14 bebês selecionados aleatoriamente, o teste t de pares deve ser usado.
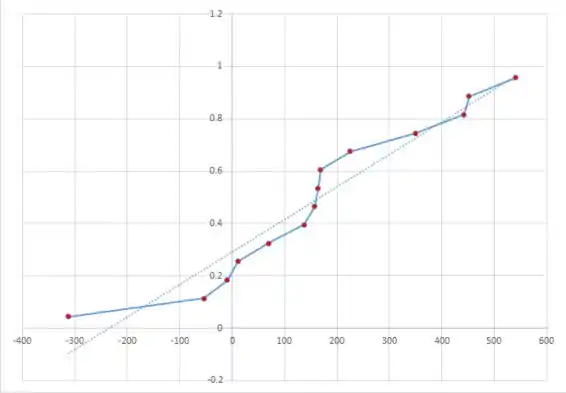
Figura 1 Gráfico de Probabilidade Normal
Passo 2
Quando (diferença entre observações dentro de um par), e hipótese nula
o valor da estatística de teste para testar as hipóteses é
Onde e são a média amostral e o desvio padrão amostral das diferenças , respectivamente. Para usar este teste, suponha que as diferenças são de uma população normal. Dependendo da hipótese alternativa, o valor de PP pode ser determinado como a área correspondente sob o curva.
As hipóteses de interesse são versus . O valor da estatística de teste pode ser obtido quando se encontra a média amostral e o desvio padrão amostral das diferenças.
Uma média amostral de observações é dado por
A média amostral para as diferenças é
O valor delta é
O único valor ausente para calcular o valor da estatística de teste é o desvio padrão da amostra das diferenças .
A Variação da Amostra é
Onde
O desvio padrão da amostra s é
A variação da amostra é
e o desvio padrão da amostra.
Passo 2
O valor da estatística de teste é
O teste é bilateral onde a hipótese alternativa é portanto, o valor de P é duas vezes a área sob o curva à direita do valor |t|
onde TT tem distribuição de alunos com 13 graus de liberdade, e a probabilidade calculada usando software (você pode usar a tabela no apêndice do livro). No nível de significância , porque
em determinado nível de significância. Há evidências suficientes para concluir que a verdadeira diferença média entre os valores dos dois métodos é diferente de 0.