Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 66
Um componente em forma de U deve ser formado a partir de três peças A, B e C. O esquema é mostrado na Fig 5.20. O comprimento de A é normalmente distribuído, com uma média de 10 milímetros e um desvio padrão de 0.1 milímetro. A espessura das peças B e C é distribuída normalmente, com uma média de 2 milímetros e um desvio padrão de 0.05 milímetros. Suponha que todas as dimensões sejam independentes.
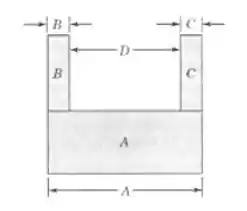
- Determine a média e o desvio padrão do comprimento da aberta D.
- Qual é a probabilidade de a abertura D ser menor do que 5.9 milímetros?
Passo 1
Sejam as variáveis aleatórias e que representam o comprimento de A, as espessuras de B e C, e o comprimento de D, respectivamente:
Letra a:
Vamos encontrar a média e o desvio padrão do comprimento da lacuna D.
=--
=++
Passo 2
Letra b:
Agora, vamos calcular a probabilidade de que a lacuna D seja menor que 5.9 mm.
Resposta
- e
- 0.2061
Exercícios de Livros Relacionados
Latas de refrigerante são cheias porque é uma máquina de enchimento automático, sendo o desvio padrão = 0.5 onças fluídas. Considere que o volume de enchimentos 10 latas sejam variáveis aleatórias nor
Na fabricação de lâmpadas de eletroluminescência, várias camadas diferentes de tinta são depositadas em um substrato plástico. As pessoas dessas camadas a crítica se especificações relativas a cor fin
X e Y são variáveis aleatórias normais e independentes, com Determine o seguinte;
Uma capa plástica para um disco magnético é composta de duas metades. A espessura de cada metade é normalmente distribuída, com uma média de 1.5 milímetro e desvio padrão de 0.1 milímetro. As duas met
A largura de um portal é distribuída normalmente, com uma média de 24 polegadas e um desvio padrão de ⅛ polegada. A largura de uma porta é normalmente distribuída, com uma média de 23 e ⅞ polegadas e