Considere os eventos a seguir para clientes que compram um conjunto de pneus em uma determinada loja, considere os eventos
A = {os pneus comprados foram fabricados nos Estados Unidos}
B = {o comprador fez o balanceamento dos pneus imediatamente}
C = {o comprador solicita alinhamento dianteiro e traseiro}
em conjunto com A’, B’ e C’. Assuma as probabilidades condicionais e não-condicionais a seguir:
a) Construa um diagrama de arvore formado por ramos de primeira, segunda e terceira gerações, identifique cada evento e a probabilidade apropriada próximo a cada ramo.
b) Calcule
c) Calcule
d) Calcule
e) Calcule , a probabilidade de uma compra de pneus americanos, dado que são solicitados alinhamento e balanceamento.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro comecemos pelo item a) montando nosso diagrama com base no enunciado e nos dados fornecidos, assim ficamos com:
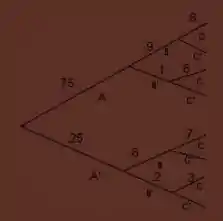
Passo 2
Vamos ao item b)
Agora com o nosso diagrama montado podemos partir a resolução do item b)
Nesse item queremos
Com base no nosso diagrama, podemos concluir que:
Passo 3
Agora, partindo ao item c)
Nesse item estamos interessados em calcular
Parece ser complicado resolver esse exercício só com o nosso diagrama, mas podemos fazer uma leve mudança que facilita nossas contas.
Numericamente ficamos com:
Passo 4
Vamos fazer o item d)
Nesse item queremos
Vamos traçar todos os caminhos para descobrir o valor de .
Assim, ficamos com:
Agora é fácil de resolver, temos todos esses valores no nosso diagrama, assim ficamos com o seguinte:
Passo 5
Vamos complementar o exercício com o item e)
Nesse item queremos calcular
Usando a relação para exercícios de probabilidade com “dado que”, temos:
Resposta
a) vide diagrama.
b)
c)
d)
e)