Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 102

Considere uma mostra e que tenhamos calculado para amostra. Agora, uma N +1/10 ésima observação se torna disponível. Seja e a média variância da amostra respectivamente, usando todas as animais observações.

  1. mostre como Xn+1 pode ser calculado, usando
  2. Mostre que
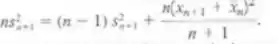
  3. Use os resultados dos itens a e b para calcular uma nova medida e desvio padrão da amostra para os dados do Exercício 6-22, quando a nova observação for x38=64

Passo 1

Letra a:

Uma boa abordagem é começar pela definição. Portanto

x ̄ n + 1 = 1 n + 1 ∑ i = 1 n + 1 x i

que é obviamente calculado de x n e x n + 1 como

x ̄ n + 1 = 1 n + 1 ( n x ̄ n + x n + 1 )

porque,

n x ̄ n = ∑ i = 1 n x i

Passo 2

Letra b:

Uma vez que se sabe o que precisa ser provado, através de todas as etapas deve-se

sempre ter isso em mente. Começando com o seguinte:

s 2 n + 1 = 1 n ∑ i = 1 n + 1 x 2 i - ∑ i = 1 n + 1 x i 2 n + 1

e

n s 2 n + 1 = ∑ i = 1 n + 1 x i 2 - ( ∑ i = 1 n + 1 x i ) 2 n + 1

No resultado, observe que temos que usar apenas s 2 n ,   x n + 1 e x ̄ n , portanto, nós separamos as somas e temos:

n s 2 n + 1 = ∑ i = 1 n + 1 x i 2 - ( ∑ i = 1 n + 1 x i ) 2 n + 1

= ∑ i = 1 n + 1 x i 2 - 1 n + 1 ( ∑ i = 1 n x i ) 2 - 2 1 n + 1 n x ̄ n × x n + 1 - 1 n + 1 x 2 n + 1

Existem duas maneiras de continuar, podemos tanto começar por trás (do resultado que temos) e chegar a este ponto, ou continuar. Nós vamos continuar. Então:

s 2 n = 1 n - 1 ( ∑ i = 1 n x i - 1 n ( ∑ i = 1 n x i ) 2 )

nós temos que

( n - 1 ) s 2 n = ∑ i = 1 n x i - 1 n ( ∑ i = 1 n x i ) 2

que queremos criar para terminar nossa equação. Então:

n s 2 n + 1 = ∑ i = 1 n x i 2 + x 2 x + 1 - 1 n + 1 x 2 n + 1 - 1 n + 1 ( ∑ i = 1 n x i ) 2 - 2 n n + 1 x ̄ n × x n + 1

= ( n - 1 ) s n + n n + 1 ( x n + 1 - x ̄ n ) 2

Passo 3

Letra c:

Do exercício 6-38, a partir dos dados e informações fornecidos, o número da média da amostra e o desvio padrão da amostra são

n = 37

x ̄ n = 65.162

s n = 2.5442

Para nosso x 38 = 64 , temos a média da amostra

x ̄ 38 = 1 38 ( 37 × 65.162 + 64 ) = 65.1314

e o desvio padrão da amostra

37 × s 2 38 = 36 × ( 2.5442 ) 2 + 37 38 ( 64 - 65.162 ) 2

que é igual a

s 38 = 2.52

Resposta

  1. x ̄ n + 1 = 1 n + 1 ( n x ̄ n + x n + 1 )
  2. = ( n - 1 ) s n + n n + 1 ( x n + 1 - x ̄ n ) 2
  3. s 38 = 2.52
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A concentração de uma solução é medida seis vezes por uma operadora que usa mesmo instrumento. Ela tem os seguintes dados: 63,2, 67,1, 65,8, 64,0 , 65,1, 65,3 g/L. Calcule a média da amostra. Suponha
Um artigo em Quality Engineering apresenta dados de viscosidade de um processo químico em batelada. Uma amostra desse estado é apresentada a seguir.
Em 1789, Henry Cavendish estimou a densidade da Terra usando uma balança de torção. Suas 29 medidas estão apresentadas a seguir, expressas como múltiplos a densidade da água.Calcule a média desvio pad
Em 1879, a. A. Michaelson fez sem determinações da velocidade da luz no ar usando uma modificação de um método proposto pelo físico francês Foucault. Em ela fez as medidas e cinco tentativas de 20 med
Uma amostra com seis resisto Oris resultou na seguinte resistências.Calcule a variância o desvio padrão da amostra. Subtraia 35 de cada uma das medidas originais de resistência e calcule. Compare os r